《孙子算经》是我国古代内容极其丰富的数学名著，书中有如下问题：“今有圆窖，周五丈四尺，深一丈八尺，问受粟几何？”其意思为：“有圆柱形容器，底面圆周长五丈四尺，高一丈八尺，求此容器能装多少斛米.”则该圆柱形容器能装米__________斛.（古制1丈=10尺，1斛=1.62立方尺，圆周率
）
科目：高中数学 来源：2017届广东省梅州市高三下学期一检（3月）数学（文）试卷（解析版） 题型：解答题
中石化集团获得了某地深海油田区块的开采权，集团在该地区随机初步勘探了部分儿口井，取得了地质资料.进入全面勘探时期后，集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高，如果新设计的井位与原有井位重合或接近，便利用旧井的地质资料，不必打这口新井，以节约勘探费用．勘探初期数据资料见如表：
（Ⅰ）1～6号旧井位置线性分布，借助前5组数据求得回归直线方程为
，求
，并估计
的预报值；
（Ⅱ）现准备勘探新井
，若通过1、3、5、7号井计算出的
的值（精确到0.01）相比于（Ⅰ）中
的值之差不超过10%，则使用位置最接近的已有旧井
，否则在新位置打开，请判断可否使用旧井？
（参考公式和计算结果：
）
（Ⅲ）设出油量与勘探深度的比值
不低于20的勘探并称为优质井，那么在原有井号1～6的出油量不低于50L的井中任意勘探3口井，求恰好2口是优质井的概率.
查看答案和解析>>
科目：高中数学 来源：2017届山东省淄博市高三3月模拟考试文数试卷（解析版） 题型：解答题
已知椭圆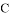
：
经过点
，离心率为
，点
为椭圆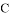的右顶点，直线
与椭圆相交于不同于点的两个点
.
（Ⅰ）求椭圆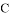的标准方程；
（Ⅱ）当
时，求
面积的最大值；
（Ⅲ）若，求证：
为定值.
查看答案和解析>>
科目：高中数学 来源：2017届河南省焦作市高三下学期第二次模拟考试数学（理）试卷（解析版） 题型：解答题
已知圆
： 
过椭圆
： 
(
)的短轴端点， 
， 
分别是圆
与椭圆
上任意两点，且线段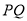
长度的最大值为3．
（Ⅰ）求椭圆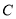
的方程；
（Ⅱ）过点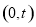
作圆
的一条切线交椭圆
于
， 
两点，求
的面积的最大值．
查看答案和解析>>
科目：高中数学 来源：2017届河南省南阳、信阳等六市高三第一次联考理数试卷（解析版） 题型：选择题
将函数
的图象向右平移
个单位后得到函数
的图象，若函数在区间
和
上均单调递增，则实数
的取值范围是 （ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2016-2017学年吉林省舒兰市高一上学期期末考试数学试卷（解析版） 题型：选择题
已知直线
：
（
）被圆
所截的弦长是圆心
到直线的距离的2倍，则
等于（ ）
A. 6 B. 8 C. 9 D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
上随机地取一个数
,则事件“
”发生的概率为 （ ）.
B. 
C. 
D. 
为矩形
所在平面内一点，
，
，
，
，则
（ ）
B. 
C. 
，则
（ ）
B. 
C. 
D. 