
(本小题13分)某工厂要建造一个无盖长方体水池,底面一边长固定为8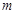 ,最大装水量为72
,最大装水量为72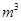 ,池底和池壁的造价分别为
,池底和池壁的造价分别为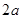 元
元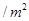 、
、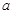 元
元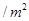 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
科目:高中数学 来源:2010年北京市崇文区高三下学期一模数学(文)测试 题型:解答题
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了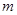 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为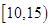 ,
,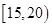 ,
,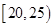 ,
,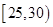 ,
,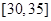 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在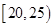 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求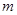 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了![]() 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
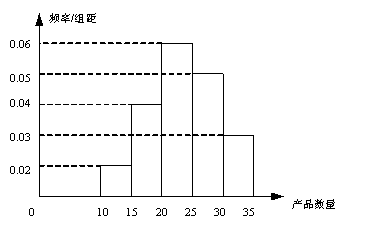
,![]() ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在![]() 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求![]() ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
 人不在同一组的概率是多少?
人不在同一组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了![]() 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
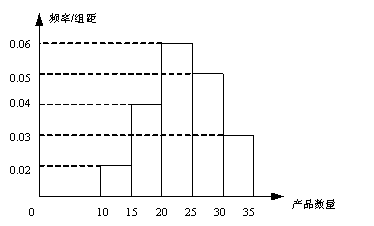
,![]() ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在![]() 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求![]() ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
 人不在同一组的概率是多少?
人不在同一组的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com