
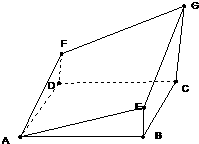
 已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,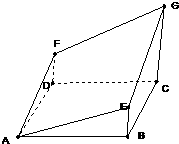 解:(1)建立如图所示的空间直角坐标系,
解:(1)建立如图所示的空间直角坐标系,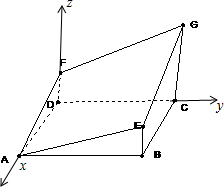
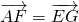 ,
,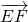 =(-2,-4,2).于是|
=(-2,-4,2).于是| |=2
|=2 ,即BF的长为2
,即BF的长为2 .
. =(-2,-4,2),
=(-2,-4,2), =(0,1,0),|cos<
=(0,1,0),|cos<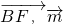 >|=
>|=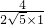 =
= =sinθ
=sinθ  ∴BF与平面BCGE所成角的正切值为tanθ=2.
∴BF与平面BCGE所成角的正切值为tanθ=2. 为平面AEGF的法向量且
为平面AEGF的法向量且  =(x,y,z)
=(x,y,z)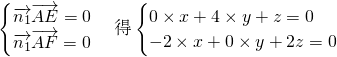
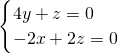 令z=1∴
令z=1∴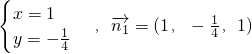 ,易知平面ABCD的法向量
,易知平面ABCD的法向量 =(0,0,1)
=(0,0,1)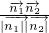 |=
|=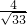
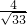 .
.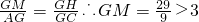 .故不存在.
.故不存在.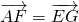 ,得到F点的坐标;利用
,得到F点的坐标;利用 与平面BCGE的法向量夹角求解.
与平面BCGE的法向量夹角求解.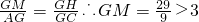 .故不存在.
.故不存在.

科目:高中数学 来源: 题型:
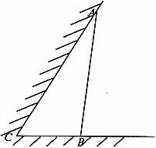
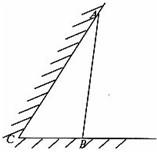 如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有的两面墙的夹角为60°(即∠C=60°且两面墙的长度足够大),现有可供建造第三面围墙的材料6米(即AB长为6米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有的两面墙的夹角为60°(即∠C=60°且两面墙的长度足够大),现有可供建造第三面围墙的材料6米(即AB长为6米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:
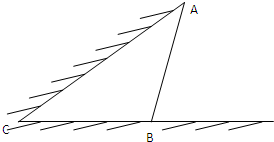 如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室.已知已有两面墙的夹角为60°(即∠C=60°),第三面围墙的长度为6米,即AB=6米,(两面墙的长均大于6米).为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大.记∠ABC=θ,问当θ为多少时,所建造的三角形露天活动室的面积最大?
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室.已知已有两面墙的夹角为60°(即∠C=60°),第三面围墙的长度为6米,即AB=6米,(两面墙的长均大于6米).为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大.记∠ABC=θ,问当θ为多少时,所建造的三角形露天活动室的面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:
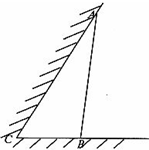 如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即∠C=60°),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即∠C=60°),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:
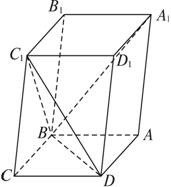
(1)求证:CC1⊥BD;
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD?并加以证明.
的值为多少时,能使A1C⊥平面C1BD?并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有两面墙的夹角为![]() (即
(即![]() ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料![]() 米(两面墙的长均大于
米(两面墙的长均大于![]() 米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记![]() ,问当
,问当![]() 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com