试题分析:(Ⅰ)依据S
n=2
n-a,根据数列的前n项和,求出数列{a
n}的通项公式,并且根据初始条件求出a=1,a
n=2
n-1,再根据b
2+5,b
4+5,b
8+5成等比数列,得出(b
4+5)
2=(b
2+5)(b
8+5),解得d=0(舍去),或d=8,从而求出{b
n}的通项公式为b
n=8n-5;(Ⅱ)由(Ⅰ)a
n=2
n-1代入log
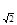
a
n=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出T
n=
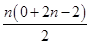
=n(n-1),而b
n=8n-5,根据T
n>b
n,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
试题解析:
(Ⅰ)当n=1时,a
1=S
1=2-a;
当n≥2时,a
n=S
n-S
n-1=2
n-1.
∵{a
n}为等比数列,
∴2-a=1,解得a=1.
∴a
n=2
n-1.
设数列{b
n}的公差为d,
∵b
2+5,b
4+5,b
8+5成等比数列,
∴(b
4+5)
2=(b
2+5)(b
8+5),
又b
1=3,
∴(8+3d)
2=(8+d)(8+7d),
解得d=0(舍去),或d=8.
∴b
n=8n-5.
(Ⅱ)由a
n=2
n-1,得log
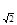
a
n=2(n-1),
∴{log
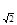
a
n}是以0为首项,2为公差的等差数列,
∴T
n=
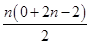
=n(n-1).
由b
n=8n-5,T
n>b
n,得
n(n-1)>8n-5,即n
2-9n+5>0,
∵n∈N
*,∴n≥9.
故所求n的最小正整数为9.

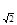 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.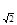 an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=
an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=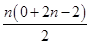 =n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
=n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.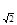 an=2(n-1),
an=2(n-1),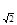 an}是以0为首项,2为公差的等差数列,
an}是以0为首项,2为公差的等差数列,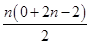 =n(n-1).
=n(n-1).
