
【题目】设![]() ,其中
,其中![]() .若
.若![]() 对一切
对一切![]() 恒成立,则①
恒成立,则①![]() ;②
;②![]() ;③
;③![]() 既不是奇函数也不是偶函数;④
既不是奇函数也不是偶函数;④![]() 的单调递增区间是
的单调递增区间是![]() ;⑤存在经过点
;⑤存在经过点![]() 的直线与函数
的直线与函数![]() 的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
【答案】①③
【解析】
对于命题①,由![]() 对一切
对一切![]() 恒成立知,直线
恒成立知,直线![]() 是
是![]() 图像的对称轴.又函数
图像的对称轴.又函数![]() 的周期为
的周期为![]() ,即
,即![]() 故①正确;
故①正确;
对于命题②,因为![]() 和
和![]() 与对称轴的距离相等,即
与对称轴的距离相等,即![]() ,故②不正确.
,故②不正确.
对于命题③,因为直线![]() 是函数图像的对称轴,易得
是函数图像的对称轴,易得![]() ,
,
即![]() 或
或![]() .即
.即![]() 即不是奇函数也是不偶函数,故③正确.
即不是奇函数也是不偶函数,故③正确.
对于命题④,由上知![]() 的解析式不确定,即单调递增区间不确定,故④不正确.
的解析式不确定,即单调递增区间不确定,故④不正确.
对于命题⑤,因为![]() (其中
(其中![]() ),
),
可得![]() ,且
,且![]() ,即过点
,即过点![]() 的直线必与函数
的直线必与函数![]() 的图像相交,故⑤不正确.
的图像相交,故⑤不正确.
解:由![]() 对一切
对一切![]() 恒成立知,直线
恒成立知,直线![]() 是
是![]() 图像的对称轴.又∵
图像的对称轴.又∵![]() (其中
(其中![]() )的周期为
)的周期为![]() ,∴
,∴![]() 可看作
可看作![]() 的值加了
的值加了![]() 个周期,∴
个周期,∴![]() .故①正确.
.故①正确.
∵![]() ,∴
,∴![]() 和
和![]() 与对称轴的距离相等.
与对称轴的距离相等.
∴![]() ,故②不正确.
,故②不正确.
∵直线![]() 是函数图像的对称轴,∴
是函数图像的对称轴,∴![]() ,
,
∴![]() .
.
∴![]() 或
或![]() ,∴
,∴![]() .∴
.∴![]() 或
或![]() .
.
∴![]() 即不是奇函数也是不偶函数,故③正确.
即不是奇函数也是不偶函数,故③正确.
由上知![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]()
![]() 的单调递增区间为
的单调递增区间为![]() .∵
.∵![]() 的解析式不确定,∴单调递增区间不确定,故④不正确.
的解析式不确定,∴单调递增区间不确定,故④不正确.
∵![]() (其中
(其中![]() ),
),
∴![]() .又∵
.又∵![]() ,∴
,∴![]() .
.
∴![]() ,且
,且![]() ,
,
∴过点![]() 的直线必与函数
的直线必与函数![]() 的图像相交,故⑤不正确.
的图像相交,故⑤不正确.
故答案为①③.


科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
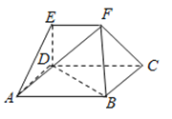
(Ⅰ)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(Ⅱ)在(Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F到左顶点的距离为3.
的右焦点F到左顶点的距离为3.
(1)求椭圆C的方程;
(2)设O是坐标原点,过点F的直线与椭圆C交于A,B两点(A,B不在x轴上),若![]() ,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为M,当M≥85时,产品为一级品;当75≤M<85时,产品为二级品;当70≤M<75时,产品为三级品.现用两种新配方(分别称为A配方和B配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表

B配方的频数分布表

(1)从A配方生产的产品中按等级分层抽样抽取5件产品,再从这5件产品中任取3件,求恰好取到1件二级品的频率;
(2)若这种新产品的利润率y与质量指标M满足如下条件: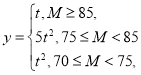 其中t∈
其中t∈![]() ,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周长为3,求△ABC的内切圆面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立![]() 周年,某车间内举行生产比赛,由甲乙两组内各随机选取
周年,某车间内举行生产比赛,由甲乙两组内各随机选取![]() 名技工,在单位时间生产同一种零件,其生产的合格零件数的茎叶图如下:
名技工,在单位时间生产同一种零件,其生产的合格零件数的茎叶图如下:
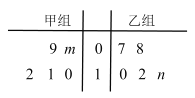
已知两组所选技工生产的合格零件的平均数均为![]() .
.
(1)分别求出![]() 的值;
的值;
(2)分别求出甲乙两组技工在单位时间内加工的合格零件的方差![]() 和
和![]() ,并由此估计两组技工的生产水平;
,并由此估计两组技工的生产水平;
(3)若单位时间内生产的合格零件个数不小于平均数的技工即为“生产能手”,根据以上数据,能否认为该车间50%以上的技工都是生产能手?
(注:方差![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2,g(x)=xlna,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=![]() -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com