[题目]设数列的前项和为.且对任意正整数.满足．(1)求数列的通项公式．(2)设.求数列的前项和．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设数列的前项和为，且对任意正整数，满足．

（1）求数列的通项公式．

（2）设，求数列的前项和．

【答案】（1）；（2）．

【解析】

试题分析：（1）由当时，，两式相减得

．又当时，

是以首项，公比的等比数列的通项公式为；（2）由（1）知，．

试题解析：（1）因为，

所以，当时，，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分

两式相减得，即．．．．．．．．．．．．．．．．3分

又当时，，即．．．．．．．．．．4分

所以是以首项，公比的等比数列，

所以数列的通项公式为．．．．．．．．．．．．．．．．．．．．．．．6分

（2）由（1）知，，．．．．．．．．．．．．．．．．．．．7分

则，①

，②．．．．．．．．．．．．．．．．．8分

②-①得

，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分

，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．11分

所以，数列的前项和为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知随机变量的取值为不大于的非负整数值，它的分布列为：

	0	1	2		n

其中（）满足：，且．

定义由生成的函数，令．

（I）若由生成的函数，求的值；

（II）求证：随机变量的数学期望，的方差；

（）

（Ⅲ）现投掷一枚骰子两次，随机变量表示两次掷出的点数之和，此时由生成的函数记为，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）将函数的图像向右平移个单位得到函数的图像，若，求函数的值域；

（2）已知，分别为中角的对边，且满足，求的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱柱ABC－A1B1C1中，△ABC是等边三角形，BC＝CC1＝4，D是A1C1中点．

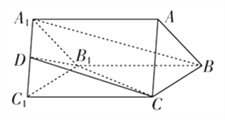
(1)求证：A1B∥平面B1CD；

(2)当三棱锥C－B1C1D体积最大时，求点B到平面B1CD的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图所示，成绩不小于90分为及格．

（Ⅰ）设甲、乙两个班所抽取的10名同学成绩方差分别为、，比较、的大小（直接写出结果，不写过程）；

（Ⅱ）从甲班10人任取2人，设这2人中及格的人数为X，求X的分布列和期望；

（Ⅲ）从两班这20名同学中各抽取一人，在已知有人及格的条件下，求抽到乙班同学不及格的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知f(x)在R上是单调递减的一次函数，且f(f(x))＝4x－1.

(1)求f(x)；

(2)求函数y＝f(x)＋x2－x在x∈[－1,2]上的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分12分）某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过）：

空气质量指数
空气质量等级	级优	级良	级轻度污染	级中度污染	级重度污染	级严重污染

该社团将该校区在年天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率．

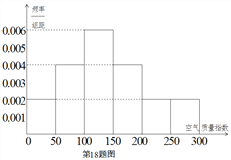
（Ⅰ）请估算年（以天计算）全年空气质量优良的天数(未满一天按一天计算)；

（Ⅱ）该校年月、日将作为高考考场，若这两天中某天出现级重度污染，需要净化空气费用元，出现级严重污染，需要净化空气费用元，记这两天净化空气总费用为元，求的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

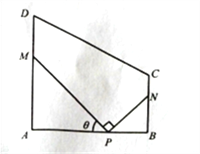
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, 百米，百米，广场入口P在AB上，且，根据规划，过点P铺设两条相互垂直的笔直小路PM,PN（小路的宽度不计），点M,N分别在边AD,BC上（包含端点），区域拟建为跳舞健身广场，区域拟建为儿童乐园，其它区域铺设绿化草坪，设.