
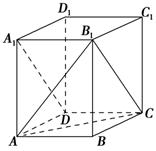
(13分)如图,正方体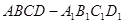 中.
中.
(Ⅰ)求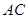 与
与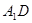 所成角的大小;
所成角的大小;
(Ⅱ)求二面角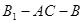 的正切值.
的正切值.
(Ⅰ)异面直线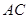 与
与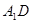 所成角为
所成角为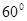 ;(Ⅱ)二面角
;(Ⅱ)二面角 的正切值为
的正切值为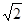 。
。
【解析】(I)连接B1C,则易证B1C//A1D,所以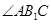 就是异面
就是异面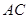 与
与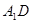 所成角,然后解三角形
所成角,然后解三角形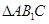 求此角即可.
求此角即可.
(II)连接BD交AC于O点,则易证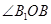 就是二面角
就是二面角 的平面角,然后再直角三角形B1BO中求此角即可.
的平面角,然后再直角三角形B1BO中求此角即可.
(Ⅰ)在正方体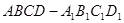 中,
中,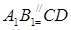 --------------------1
--------------------1
∴A1B1CD为平行四边形,∴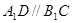 ,--------------------------- 2
,--------------------------- 2
所以∠ACB1或其补角即异面直线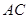 与
与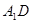 所成角………………3
所成角………………3
设正方形边长为
在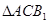 中,AC=B1A=B1C=
中,AC=B1A=B1C= ,………………………….5
,………………………….5
∴∠ACB1=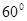
所以异面直线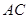 与
与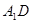 所成角为
所成角为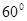 ……………………………..6
……………………………..6
(Ⅱ)连结BD交AC于O,连结B1O,…………………………………….7
∵O为AC中点, B1A=B1C,BA=BC
∴B1O⊥AC,BO⊥AC………………………………….9
∴∠B1OB为二面角 的平面角.---------------------------10
的平面角.---------------------------10
在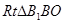 中, B1B=
中, B1B= ,BO=
,BO=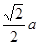 --------------------12
--------------------12
∴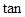 ∠B1OB=
∠B1OB=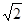
故二面角 的正切值为
的正切值为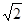 ---------------------13.
---------------------13.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴,| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OA |
| OB |
| e1 |
| OA |
| e1 |
| OB |
| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com