
分析 由f(-2+x)=f(-2-x)得出对称轴x=-2,由题意得f(x)的图象与x轴的交点坐标为(0,0)(-4,0),设f(x)=ax(x+4),利用一元二次方程根的问题求出a的值.
解答 解:∵二次函数f(x)满足f(-2+x)=f(-2-x),
∴对称轴x=-2,
∵f(x)的图象被x轴截得的线段长为4,
∴f(x)的图象与x轴的交点坐标为(0,0)(-4,0),
∴设f(x)=ax(x+4)=ax2+4ax,
∵方程f(x)=x有唯一的等根,
∴ax2+(4a-1)x=0有唯一的等根.
即△=(4a-1)2=0,解得a=$\frac{1}{4}$,
∴f(x)=$\frac{1}{4}$x2+x.
点评 本题考查了二次函数的解析式,二次函数的性质,方程的根,一元二次函数图象的交点问题,属于中档题.


科目:高中数学 来源: 题型:解答题
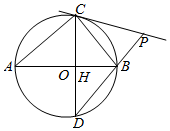 如图,△ABC内接于⊙O,AB为其直径,CH⊥AB于H延长后交⊙O于D,连接DB并延长交过C点的直线于P,且CB平分∠DCP.
如图,△ABC内接于⊙O,AB为其直径,CH⊥AB于H延长后交⊙O于D,连接DB并延长交过C点的直线于P,且CB平分∠DCP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
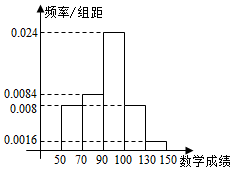 语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图:
语文成绩服从正态分布N(100,17.52),数学成绩的频率分布直方图如图:| P(k2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com