
(本小题满分14分)若函数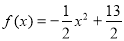 在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
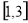 或
或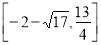
【解析】
试题分析:(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解题的关键是对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论;(2)二次函数、二次方程与二次不等式统称“三个”二次,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法,一般从:①开口方向;②对称轴位置;③判别式;④端点值符合四个方面分析;(3)二次函数的综合问题应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想,
试题解析: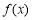 在
在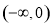 上单调递增,在
上单调递增,在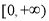 上单调递减. (1分)
上单调递减. (1分)
(1)当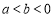 时,假设有
时,假设有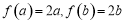 , (2分)
, (2分)
则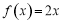 在
在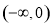 上有两个不等的实根a,b. (4分)
上有两个不等的实根a,b. (4分)
由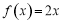 得
得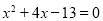 ,
,
因为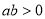 ,所以
,所以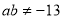 ,故假设不成立. (5分)
,故假设不成立. (5分)
(2)当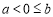 时,假设有
时,假设有 ,即
,即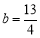 . (6分)
. (6分)
当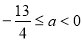 时,
时, ,得
,得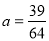 不符合; (7分)
不符合; (7分)
当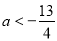 时,
时,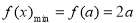 , (8分)
, (8分)
解得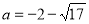 或
或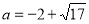 (舍去). (9分)
(舍去). (9分)
(3)当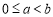 时,假设有
时,假设有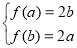 ,即
,即 (11分)
(11分)
解得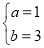 . (13分)
. (13分)
综上所述所求区间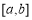 为
为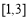 或
或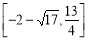 (14分)
(14分)
考点:一元二次函数在闭区间上的最值.


科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
已知不等式组 ,则目标函数z=2y﹣x的最大值是( )
,则目标函数z=2y﹣x的最大值是( )
A.1 B.﹣1 C.﹣5 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考理科数学试卷(解析版) 题型:选择题
数列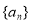 中,
中,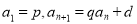 (
( N*,
N*,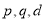 是常数),则
是常数),则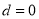 是数列
是数列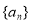 成等比数列的( )
成等比数列的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟文科数学试卷(解析版) 题型:选择题
若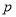 是真命题,
是真命题,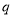 是假命题,则
是假命题,则
A.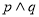 是真命题 B.
是真命题 B.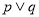 是假命题 C.
是假命题 C.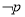 是真命题 D.
是真命题 D.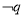 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟理科数学试卷(解析版) 题型:填空题
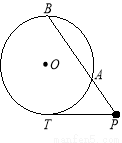
(几何证明选讲选做题)如图,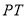 是圆
是圆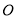 的切线,
的切线,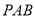 是圆
是圆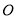 的割线,若
的割线,若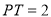 ,
,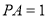 ,
,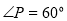 ,则圆
,则圆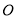 的半径
的半径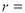 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟理科数学试卷(解析版) 题型:选择题
集合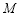 由满足:对任意
由满足:对任意 时,都有
时,都有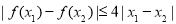 的函数
的函数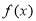 组成.对于两个函数
组成.对于两个函数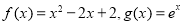 ,以下关系成立的是
,以下关系成立的是
A.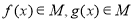 B.
B.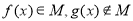
C. D.
D.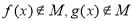
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:填空题
在平面直角坐标系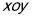 中,设
中,设 是由不等式组
是由不等式组 表示的区域,
表示的区域, 是到原点的距离不大于
是到原点的距离不大于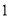 的点构成的区域,向
的点构成的区域,向 中随机投一点,则所投点落在
中随机投一点,则所投点落在 中的概率是 .
中的概率是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省德阳市四校高三联合测试(3月)理科数学试卷(解析版) 题型:填空题
已知两个不相等的非零向量 ,
,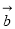 ,两组向量
,两组向量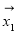 、
、 、
、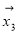 、
、 、
、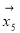 和
和 、
、 、
、 、
、 、
、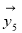 均由2个
均由2个 和3个
和3个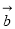 排列而成.记S=
排列而成.记S= +
+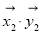 +
+ +
+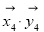 +
+ ,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .
,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .
①S有5个不同的值;②若 ⊥
⊥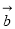 ,则Smin与
,则Smin与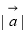 无关;
无关;
③若 ∥
∥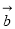 ,则Smin与
,则Smin与 无关;④若
无关;④若 ,则Smin>0;
,则Smin>0;
⑤若 ,Smin=
,Smin=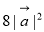 ,则
,则 与
与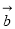 的夹角为
的夹角为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com