
(1)当AC、CD、DB满足怎样的关系时,△ACP ∽△PDB?
(2)当△ACP ∽△PDB时,求∠APB的度数.
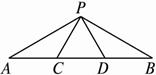
图1-11
思路分析:本题是一个探索型的问题,考查相似三角形的判定及性质,它给出了一个条件,让你自己再添加一个条件,可使两个三角形相似,因此,首先想到相似的判定方法,因又限制了三条边的关系,所以是对应边就成比例.当三角形相似了,那么对应角相等,易求∠APB.
解:(1)∵△PCD是等边三角形,?
∴∠PCD=∠PDC=60°,PD =PC =CD.?
从而∠ACP =∠PDB =120°.?
∴当![]() =
=![]() 时,△ACP∽△PDB,?
时,△ACP∽△PDB,?
即当CD2=AC·BD时,△ACP∽△PDB.?
(2)当△ACP∽△PDB时,∠APB =∠APC+∠CPD +∠DPB?
=∠PBD +60°+∠DPB?
=60°+60°=120°.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 如图,已知点P为椭圆
如图,已知点P为椭圆| x2 |
| 25 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
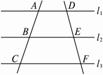
图1-2-11
A.![]() =
=![]() B.
B.![]() =
=![]() C.
C.![]() =
=![]() D.
D.![]() =
=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:

图2-11
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2012年江苏省高一上学期开学考试数学 题型:解答题
(本题11分)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则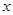 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图3,抛物线上是否存在一点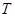 ,过点
,过点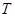 作
作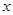 轴的垂线,垂足为
轴的垂线,垂足为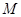 ,过点
,过点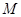 作直线
作直线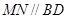 ,交线段
,交线段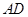 于点
于点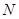 ,连接
,连接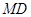 ,使
,使 ~
~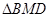 ,若存在,求出点
,若存在,求出点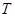 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
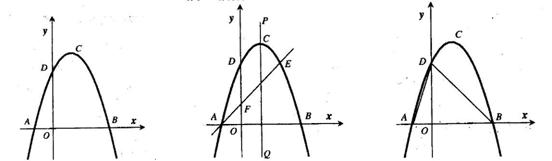 图1
图2
图3
图1
图2
图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com