Question

设函数y=f(x)是定义在R上的函数，当x＜0时，f(x)＞1,对任意实数x、y∈R,有f(x+y)=f(x)·f(y).

(1)求证：f(0)=1,且当x＞0时，有0＜f(x)＜1;

(2)若数列{a_n}满足a₁=f(0),且f(a_n+1)=,n∈N^*.

①求a_n;

②若不等式（1+)(1+)…(1+)≥k,对于n∈N^*都成立，求k的最大值.

Answer 1

(1)证明：令x=0，y=-1,则f(-1)=f(0)·f(-1).∵f(-1)＞1,

∴f(0)=1,

    又当x＞0时，-x＜0,f(-x)＞1,

    而f(x)·f(-x)=f(0)=1,∴f(-x)=＞1.

∴0＜f(x)＜1.

(2)①a₁=f(0)=1,f(a_n+1）·f(-a_n-2)=1,∴f(a_n+1-a_n-2)=1.

由已知条件及第（1）小题的结论知，只能有：

a_n+1-a_n-2=0,∴a_n+1-a_n=2,

a_n=2n-1.

②∵＞0,∴原问题可转化为：

k≤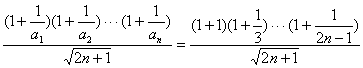,对n∈N^*都成立.

    令C_n=(1+1)(1+)…(1+),容易证明C_n+1＞C_n

    即{C_n}为递增数列，因此K≤C₁=.

∴k_max=.