
(本小题满分12)某电视机厂计划在下一个生产周期内生产两种型号电视机,每台A型或B型电视机所得利润分别为6和4个单位,而生产一台A型或B型电视机所耗原料分别为2和3个单位;所需工时分别为4和2个单位,如果允许使用的原料为100单位,工时为120单位,且A或B型电视和产量分别不低于5台和10台,应当生产每种类型电视机多少台,才能使利润最大?
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
某厂有一面旧墙长14米,现在准备利用这面旧墙建造平面图形为矩形,面积为126平方米的厂房,工程条件是①建1米新墙费用为a元;②修1米旧墙的费用为![]() 元;③拆去1米旧墙,用所得材料建1米新墙的费用为
元;③拆去1米旧墙,用所得材料建1米新墙的费用为![]() 元,经过讨论有两种方案: (1)利用旧墙的一段x米(x<14)为矩形厂房一面的边长;(2)矩形厂房利用旧墙的一面边长x≥14.问如何利用旧墙,即x为多少米时,建墙费用最省?(1)、(2)两种方案哪个更好?
元,经过讨论有两种方案: (1)利用旧墙的一段x米(x<14)为矩形厂房一面的边长;(2)矩形厂房利用旧墙的一面边长x≥14.问如何利用旧墙,即x为多少米时,建墙费用最省?(1)、(2)两种方案哪个更好?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省丹东市宽甸二中高二下学期期末考试数学(理) 题型:解答题
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数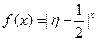 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省丹东市高二上学期期末考试文数试卷(解析版) 题型:解答题
(本小题满分12分) 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N*)间的关系为P= ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届云南楚雄州东兴中学高二上期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
某工厂修建一个长方体无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的 造价为150元,池壁每平方米的造价为120元.设池底长方形长为 米.
米.
(1)求底面积,并用含 的表达式表示池壁面积;
的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年吉林省吉林市高三2月质量检测理科数学 题型:解答题
(本小题满分12分)
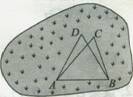
某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com