练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，海岸线上有相距5海里的两座灯塔A、B，灯塔B位于灯塔A的正南方向，海上停泊着两艘轮船，甲船位于灯塔A的北偏西60°方向，与A相距6海里的C处；乙船位于灯塔B的北偏西60°方向，与B相距10海里的D处，则两艘船之间的距离为    海里．
    【答案】分析：先连接AD，可得到AD的长度和∠DAB的值，再由余弦定理将题中数据代入即可得到答案．
    解答：解：连接AD，由题意可知AB=5，∠ABD=60°，BD=10，
    根据余弦定理可得AD=
    在三角形ACD中，CD2=AC2+AD2-2×AC×AD×cos∠CAD=21
    故答案为：
    点评：本题以实际问题为载体，考查解三角形，主要考查余弦定理的应用．属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，海岸线上有相距5海里的两座灯塔A、B，灯塔B位于灯塔A的正南方向，海上停泊着两艘轮船，甲船位于灯塔A的北偏西60°方向，与A相距6海里的C处；乙船位于灯塔B的北偏西60°方向，与B相距10海里的D处，则两艘船之间的距离为
    		21
    		21
    海里．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    如图所示，一座小岛距离海岸线上最近的点P的距离是2km，从点P沿海岸正东12km处有一个城镇．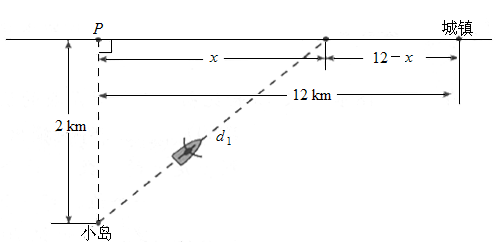

    (1)假设一个人驾驶的小船的平均速度为3km/h，步行的速度是5km/h，t(单位：h)表示他从小岛到城镇的时间，x(单位：km)表示此人将船停在海岸处距P点的距离．请将t表示为x的函数．

    (2)如果将船停在距点P4km处，那么从小岛到城镇要多长时间(精确到1h)？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图所示，海岸线上有相距5海里的两座灯塔A、B，灯塔B位于灯塔A的正南方向，海上停泊着两艘轮船，甲船位于灯塔A的北偏西60°方向，与A相距6海里的C处；乙船位于灯塔B的北偏西60°方向，与B相距10海里的D处，则两艘船之间的距离为________海里．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分12分）

    如图所示，一辆汽车从点出发，沿海岸线一条直线公路以100千米/小时的速度向东匀速行驶，汽车开动时，在距点500千米，且与海岸线距离400千米的海面上点处有一艘快艇与汽车同时出发，要把一件重要物品送给这辆汽车司机。该快艇至少以多大的速度行驶，才能将物品送到汽车司机手中？并求出快艇所行驶的距离。

    查看答案和解析>>

    同步练习册答案