某软件公司新开发一款游戏软件.该软件按游戏的难易程度共设置若干关的闯关游戏.为了激发闯关热情.每闯过一关都奖励若干慧币．设第n关奖励an个慧币.且满足$\frac{1}{2}$an≤an+1≤4an.a1=1.该软件提供了两种奖励方案:第一种.从第二关开始.每闯过一关奖励的慧币数是前一关的q倍,第二种.从第二关开始每一� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

1．某软件公司新开发一款游戏软件，该软件按游戏的难易程度共设置若干关的闯关游戏，为了激发闯关热情，每闯过一关都奖励若干慧币（一种网络虚拟币）．设第n关奖励a_n个慧币，且满足$\frac{1}{2}$a_n≤a_n+1≤4a_n，a₁=1，该软件提供了两种奖励方案：第一种，从第二关开始，每闯过一关奖励的慧币数是前一关的q倍；第二种，从第二关开始每一关比前一关多奖励d慧币（d∈R）；游戏规定：闯关者须于闯关前任选一种奖励方案．
（Ⅰ）若选择第一种方案，设第一关到第n关奖励的总慧币数为S_n，即S_n=a₁+a₂+…+a_n，且$\frac{1}{2}$S_n≤S_n+1≤
4S_n，求q的取值范围；
（Ⅱ）如果选择第二种方案，且设置第一关到第k关奖励的总币数为100（即a₁+a₂+a₃+…+a_k=100，k∈N^*）时获特别奖，为了增加获特别奖的难度，如何设置d的取值，使得k最大，并求k的最大值．

分析（Ⅰ）由题意可得第一方案{a_n}是等比数列，先根据$\frac{1}{2}$a_n≤a_n+1≤4a_n，a₁=1，求出q的范围，再根据条件和等比数列的求和公式和$\frac{1}{2}$S_n≤S_n+1≤4S_n，分类讨论，即可求出q的范围，
（Ⅱ）选择第二种方案{a_n}是等差数列，先根据$\frac{1}{2}$a_n≤a_n+1≤4a_n，a₁=1，求出d和n的关系，再根据等差数列的求和公式和a₁+a₂+a₃+…+a_k=100，即可求出答案

解答解：（Ⅰ）由题意可得第一方案{a_n}是等比数列，且$\frac{1}{2}$a_n≤a_n+1≤4a_n，a₁=1，
∴$\frac{1}{2}$q^n-1≤qⁿ≤4q^n-1，
∴$\left\{\begin{array}{l}{{q}^{n-1}（q-\frac{1}{2}）≥0}\\{{q}^{n-1}（q-4）≤0}\end{array}\right.$，
解得$\frac{1}{2}$≤q≤4，
∵$\frac{1}{2}$S_n≤S_n+1≤4S_n，当q=1时，$\frac{n}{2}$≤n+1≤4n，对任意n∈N*恒成立，故满足题意，
当q≠1时，$\frac{1}{2}$•$\frac{1-{q}^{n}}{1-q}$≤$\frac{1-{q}^{n+1}}{1-q}$≤4•$\frac{1-{q}^{n}}{1-q}$，
∴当q∈[$\frac{1}{2}$，1）时，$\left\{\begin{array}{l}{{q}^{n}（2q-1）≤1}\\{{q}^{n}（q-4）≥-3}\end{array}\right.$，由单调性可得$\left\{\begin{array}{l}{q（2q-1）≤1}\\{{q}^{\;}（q-4）≥-3}\end{array}\right.$，解得$\frac{1}{2}$≤q＜1，
当q∈（1，4]时，$\left\{\begin{array}{l}{{q}^{n}（2q-1）≥1}\\{{q}^{n}（q-4）≤-3}\end{array}\right.$，由单调性可得$\left\{\begin{array}{l}{q（2q-1）≥1}\\{q（q-4）≤-3}\end{array}\right.$，
解得1＜q≤3，
综上所述q∈[$\frac{1}{2}$，3]，
（Ⅱ）选择第二种方案{a_n}是等差数列，且$\frac{1}{2}$a_n≤a_n+1≤4a_n，a₁=1，
∴$\frac{1}{2}$[1+（n-1）d≤1+nd≤4（1+（n-1）d），
∴$\left\{\begin{array}{l}{d（n+1）≥-1}\\{d（3n-4）≥-3}\end{array}\right.$，n=1，2，3，…，k-1，
∴当n=1时，-$\frac{1}{2}$≤d≤3，
当2≤n≤k-1时，d≥$\frac{-1}{n+1}$，
∵n≤k-1，
∴d≥$\frac{-1}{d}$≥$-\frac{1}{2}$，
∵d≥$\frac{-3}{3n-4}$，
∴d≥$\frac{-3}{3k-7}$，
而-$\frac{1}{k}$≥$\frac{-3}{3k-7}$，
∴d∈[-$\frac{1}{k}$，3]，
∵a₁+a₂+…+a_k=100
∴S_k=$\frac{d}{2}$k²+（1-$\frac{d}{2}$）k=100，
∴d=$\frac{200-2k}{{k}^{2}-k}$，
∴$\frac{200-2k}{{k}^{2}-k}$∈[-$\frac{1}{k}$，3]，
解得k∈[9，199]，k∈Z，
∴k的最大值为199，且k取最大值时d=-$\frac{1}{199}$．

点评本题考查数列知识在生产实际中的具体运用，解题时要认真审题，注意挖掘题设中的隐含条件，仔细分析题设中的数量关系，合理地进行等价转化，属于难题

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

10．一圆锥的母线长为20，母线与轴的夹角为30°，则圆锥的表面积为300π．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．函数$f（x）=\left\{{\begin{array}{l}{a•sin（\frac{πx}{2}+\frac{π}{6}）}\\{{2^{-x}}}\end{array}}\right.\begin{array}{l}{（x≥0）}\\{（x＜0）}\end{array}$，若f[f（-1）]=1，则a的值是（　　）

A．

B．

-2

C．

$\frac{{2\sqrt{3}}}{3}$

D．

$-\frac{{2\sqrt{3}}}{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．曲线y=x⁴与直线y=4x+b相切，则实数b的值是-3．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2c（c＞0），左焦点为F，点M的坐标为（-2c，0）．若椭圆E上存在点P，使得PM=$\sqrt{2}$PF，则椭圆E离心率的取值范围是[$\frac{\sqrt{3}}{3}，\frac{\sqrt{2}}{2}$]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．

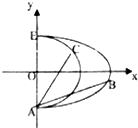已知曲线C₁：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，x≥0）和曲线C₂：x²+y²=r²（x≥0）都过点A（0，-1），且曲线C₁所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$
（1）求曲线C₁，C₂的方程
（2）设点B，C分别在曲线C₁，C₂上，k₁，k₂分别为直线AB，AC的斜率，当k₂=4k₁时，
①直线BC是否经过定点？请说明理由
②设E（0，1），求|$\overrightarrow{BC}$|•|$\overrightarrow{BE}$|的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．已知矩阵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$
（1）求矩阵M的逆矩阵M^-1；
（2）求曲线|x|+|y|=1在矩阵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$对应的变换作用下得到的曲线C方程；
（3）求曲线C所围成图形的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{x-2y+2≥0}\end{array}\right.$且a∈（-6，3），则z=$\frac{y}{x-a}$仅在点A（-1，$\frac{1}{2}$）处取得最大值的概率为（　　）

A．

$\frac{1}{9}$

B．

$\frac{2}{9}$

C．

$\frac{1}{3}$

D．

$\frac{4}{9}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．已知$f（x）=\frac{{a•{2^x}+a-2}}{{{2^x}+1}}$（x∈R），若f（x）满足f（-x）+f（x）=0，
（1）求实数a的值及f（3）；
（2）判断函数的单调性，并加以证明．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学