
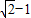 函数f(x)=
函数f(x)= 其中
其中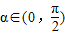
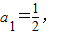 an+1=f(an)(n∈N*)求证:
an+1=f(an)(n∈N*)求证: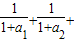 …+
…+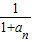 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).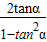 =
=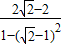 =1,将tanα=
=1,将tanα=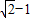 代入可求解,由α为锐角,得α,进而求得函数表达式.
代入可求解,由α为锐角,得α,进而求得函数表达式.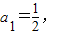 an+1=f(an)(n∈N*),知
an+1=f(an)(n∈N*),知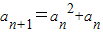 ,由此能够证明an+1>an(n∈N*).
,由此能够证明an+1>an(n∈N*).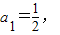 ,
,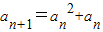 =an(an+1),能够导出
=an(an+1),能够导出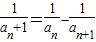 ,利用裂项求和法得到
,利用裂项求和法得到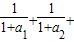 …+
…+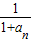 =2-
=2-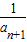 ,由此能够证明1<
,由此能够证明1<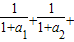 …+
…+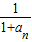 <2(n≥2,n∈N*)
<2(n≥2,n∈N*)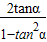 =
=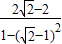 =1
=1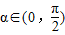 ,
,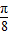 ,∴sin(2α+
,∴sin(2α+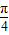 )=1,
)=1,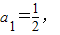 an+1=f(an)(n∈N*),
an+1=f(an)(n∈N*),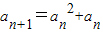 ,
,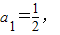 ,
,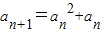 =an(an+1),
=an(an+1),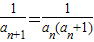 =
=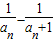 ,
,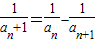 ,
,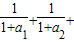 …+
…+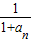 =(
=(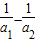 )+(
)+(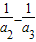 )+…+(
)+…+(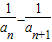 )
)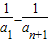
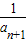 ,
,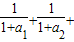 …+
…+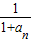 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinB+sinC |
| cosB+cosC |
| π |
| 2 |
| π |
| 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com