解:(Ⅰ)在△ABC中,由sinB+sinC=

sinA及正弦定理得:b+c=

a①(3分)
又周长a+b+c=

+1②,
由①②联立解得:a=1,即BC=1;(6分)
(Ⅱ)△ABC的面积S=

bcsinA,即

bcsinA=

sinA,所以bc=

,(8分)
又结合(Ⅰ)知,b+c=

+1-a=

,
∴在△ABC中由余弦定理得:
cosA=

(10分)
=
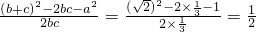
,(12分)
又△ABC的内角A∈(0,π),所以A=

,(13分)
所以△ABC的面积S=

sinA=

×sin

=
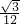
.(15分)
分析:(Ⅰ)设出三角形的三边长分别为a,b,c,根据已知的周长表示出关于a,b,c的关系式,记作②,利用正弦定理化简已知的等式,得到关于a,b,c的关系式,记作①,把①代入②即可求出a的值,进而BC的值;
(Ⅱ)利用三角形的面积公式表示出△ABC的面积S,与已知的面积相等得到一个等式,化简可得bc的值,由(Ⅰ)中的①和a的值求出b+c的值,利用余弦定理表示出cosA,变形后把b+c,bc以及a的值代入即可求出cosA的值,由A的范围,利用特殊角的三角函数值求出A的度数,将sinA的值代入已知的面积S=

sinA中即可求出△ABC的面积.
点评:此题综合考查了正弦、余弦定理以及三角形的面积公式.本题的关键是第(Ⅱ)中灵活变换cosA的表达式,注意整体代入方法的运用.同时要求学生善于发现两问之间的联系,从而建立已知与未知之间的关系.

 ,且
,且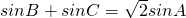 .
. ,求△ABC的面积S.
,求△ABC的面积S. sinA及正弦定理得:b+c=
sinA及正弦定理得:b+c= a①(3分)
a①(3分) +1②,
+1②, bcsinA,即
bcsinA,即 bcsinA=
bcsinA= sinA,所以bc=
sinA,所以bc= ,(8分)
,(8分) +1-a=
+1-a= ,
, (10分)
(10分)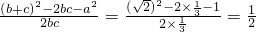 ,(12分)
,(12分) ,(13分)
,(13分) sinA=
sinA= ×sin
×sin =
=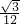 .(15分)
.(15分) sinA中即可求出△ABC的面积.
sinA中即可求出△ABC的面积.
