
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上的一点A(2,4).
(Ⅰ)是否存在直线l:y=kx+3与圆M有两个交点B,C,并且|AB|=|AC|,若有,求此直线方程,若没有,请说明理由;
(Ⅱ)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() =
= ![]() ,求实数t的取值范围.
,求实数t的取值范围.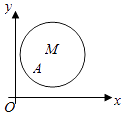
【答案】解:(Ⅰ)圆M:x2+y2﹣12x﹣14y+60=0化为(x﹣6)2+(y﹣7)2=25,圆心为M(6,7),半径为5
假设存在直线l:y=kx+3与圆M有两个交点B,C,并且|AB|=|AC|,
则AM⊥BC,∵kAM= ![]() ,即直线l的斜率为﹣
,即直线l的斜率为﹣ ![]()
则直线l:y=﹣ ![]() x+3,即4x+3y﹣9=0
x+3,即4x+3y﹣9=0
圆心M(6,7)到4x+3y﹣9=0的距离d= ![]()
即直线l与圆M无两个交点,
∴不存在直线l:y=kx+3与圆M有两个交点B,C,并且|AB|=|AC|;
(Ⅱ)设P(x1,y1),Q(x2,y2),∵A(2,4),T(t,0),
由 ![]() =
= ![]() 得,
得, ![]() ,由点Q在圆M上,所以(x2﹣6)2+(y2﹣7)2=25
,由点Q在圆M上,所以(x2﹣6)2+(y2﹣7)2=25
即得(x1﹣t﹣4)2+(y1﹣3)2=25.
从而圆(x﹣6)2+(y﹣7)2=25与圆(x﹣t﹣4)2+(y﹣3)2=25上有公共点,
即5﹣5 ![]()
解得2﹣2 ![]() ≤t≤2+2
≤t≤2+2 ![]() ,
,
∴实数t的取值范围为[2﹣2 ![]() ,2+2
,2+2 ![]() ].
].
【解析】(1)假设存在直线l:y=kx+3,由题意|AB|=|AC|,则AM⊥BC,即直线l的斜率为![]() ,根据点到直线的距离即可判断出不存在这样的直线与圆有两个交点,(2)设P(x1,y1),Q(x2,y2),由向量关系表示出Q点坐标,由于点Q在圆上,可得(x1﹣t﹣4)2+(y1﹣3)2=25,若两圆有公共点,则两圆心间的距离小于半径之和,大于半径之差,即可得到实数t的取值范围.
,根据点到直线的距离即可判断出不存在这样的直线与圆有两个交点,(2)设P(x1,y1),Q(x2,y2),由向量关系表示出Q点坐标,由于点Q在圆上,可得(x1﹣t﹣4)2+(y1﹣3)2=25,若两圆有公共点,则两圆心间的距离小于半径之和,大于半径之差,即可得到实数t的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.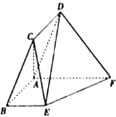
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线2x+y﹣k=0(k>0)与圆x2+y2=4交于不同的两点A,B,O是坐标原点,且有| ![]() |
| ![]() |
| ![]() |,那么k的取值范围是( )
|,那么k的取值范围是( )
A.[ ![]() ,+∞)
,+∞)
B.[ ![]() ,2
,2 ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,2
,2 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,Sn=2n﹣an(n∈N*).
(1)计算a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=lnx
(1)若曲线h(x)=f(x)+ax2﹣ex(a∈R)在点(1,h(1))处的切线垂直于y轴,求函数h(x)的单调区间;
(2)若函数 ![]() 在区间(0,2)上无极值,求实数a的取值范围.
在区间(0,2)上无极值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的袋子装有4个完全相同的小球,球上分别标有数字为0,1,2,2,现甲从中摸出一个球后便放回,乙再从中摸出一个球,若摸出的球上数字大即获胜(若数字相同则为平局),则在甲获胜的条件下,乙摸1号球的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的半径分别2 cm和5 cm,圆台的母线长是12 cm,求圆锥SO的母线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com