
 | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 |  | $\frac{1}{4}$ | $\frac{3}{4}$ |
| 型号 | A | B | C |
| 补贴金额(百元/台) | 3 | 4 | 5 |
分析 (1)仔细阅读表格得出方程组$\left\{\begin{array}{l}\frac{3}{4}q=\frac{3}{10}\\ p+q+\frac{1}{5}=1\end{array}\right.$,求解即可.
(2)确定随机变量X可能取值为7,8,9,10.求解相应的概率,列出分布列,再运用数学期望公式求解即可.
解答 解:(1)由题意得$\left\{\begin{array}{l}\frac{3}{4}q=\frac{3}{10}\\ p+q+\frac{1}{5}=1\end{array}\right.$所以$p=\frac{2}{5},q=\frac{2}{5}$.
(2)X可能取值为7,8,9,10.
$P(X=7)=\frac{1}{5}×\frac{1}{4}=\frac{1}{20}$,$P(X=8)=\frac{1}{5}×\frac{3}{4}+\frac{2}{5}×\frac{1}{4}=\frac{1}{4}$,$P(X=9)=\frac{2}{5}×\frac{1}{4}+\frac{2}{5}×\frac{3}{4}=\frac{2}{5}$; $P(X=10)=\frac{2}{5}×\frac{3}{4}=\frac{3}{10}$.
所以X的分布列为:
| X | 7 | 8 | 9 | 10 |
| P | $\frac{1}{20}$ | $\frac{1}{4}$ | $\frac{2}{5}$ | $\frac{3}{10}$ |
点评 考察了图表格的运用,分析能力,计算化简能力,属于难题,关键是掌握好随机变量的概率的关系,列出方程组.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 70 | B. | 84 | C. | 140 | D. | 420 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
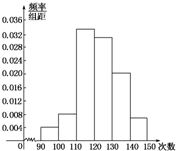 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个白球;都是白球 | B. | 两个白球;至少有一个红球 | ||
| C. | 红球、白球各一个;都是白球 | D. | 红球、白球各一个;至少有一个白球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com