解:(1)∵函数
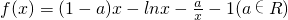
∴f′(x)=
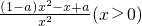
∵曲线y=f(x)在x=1和x=3处的切线互相平行,
∴f′(1)=f′(3),
∴

∴6-8a=0
∴a=

;
(2)若a=1时,

,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0
∴y=f(x)在(0,1)上为增函数,在(1,+∞)上为减函数;
若a≠1时,令f′(x)=0,可得x
1=1,x
2=
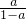
①若
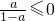
,则a≥1,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0
∴y=f(x)在(0,1)上为增函数,在(1,+∞)上为减函数;
②若

0,即0<a<1时
(Ⅰ)0<

时,

1,在(0,
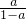
),(1,+∞)上为增函数,在(
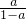
,1)上为减函数
(Ⅱ)

时,在(0,1),(
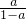
,+∞)上为增函数,在(1,
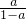
)上为减函数
(Ⅲ)

时,f′(x)>0恒成立,则f(x)在(0,+∞)上恒为增函数.
(3)当

时,由(1)知,函数

在 (0,1)是增函数,在(1,2)是减函数
∴f(x)在(0,2]的最大值为f(1)=-

若对任意x
1∈(0,2],都存在x
2∈(0,2],都存在x
2∈[1,2]使f(x
1)≤g(x
2),等价于函数f(x)在(0,2]的最大值-

不大于g(x)在[1,2]的最大值
下面求g(x)=x
2-bx+1在[1,2]上的最大值
∵g(x)=x
2-bx+1的对称轴是直线

①当
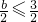
,即b≤3时,g(x)在[1,2]为增函数,则g(x)
max=g(2)=5-2b,
∴

,∴b≤

,满足b≤3;
②当
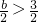
,即b>3时,g(x)在[1,2]为减函数,则g(x)
max=g(1)=2-b,
∴
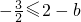
,∴b≤

,∴3<b≤

,
综上,实数b的取值范围为b≤

.
分析:(1)求导数,利用曲线y=f(x)在x=1和x=3处的切线互相平行,即可求得a的值;
(2)若a=1时,利用导数的正负可得y=f(x)在(0,1)上为增函数,在(1,+∞)上为减函数;
若a≠1时,令f′(x)=0,可得x
1=1,x
2=
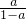
,结合函数的定义域分类讨论,即可求得结论;
(3)当

时,f(x)在(0,2]的最大值为f(1)=-

,若对任意x
1∈(0,2],都存在x
2∈(0,2],都存在x
2∈[1,2]使f(x
1)≤g(x
2),等价于函数f(x)在(0,2]的最大值-

不大于g(x)在[1,2]的最大值,利用配方法确定函数g(x)=x
2-bx+1在[1,2]上的最大值,即可得到实数b的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

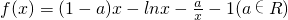
 时,设g(x)=x2-bx+1,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),求实数b的取值范围.
时,设g(x)=x2-bx+1,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),求实数b的取值范围.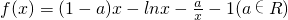
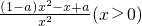

 ;
; ,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0
,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0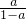
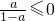 ,则a≥1,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0
,则a≥1,∴x∈(0,1),f′(x)>0,x∈(1,+∞),f′(x)<0 0,即0<a<1时
0,即0<a<1时 时,
时, 1,在(0,
1,在(0,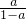 ),(1,+∞)上为增函数,在(
),(1,+∞)上为增函数,在(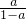 ,1)上为减函数
,1)上为减函数 时,在(0,1),(
时,在(0,1),(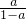 ,+∞)上为增函数,在(1,
,+∞)上为增函数,在(1,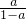 )上为减函数
)上为减函数 时,f′(x)>0恒成立,则f(x)在(0,+∞)上恒为增函数.
时,f′(x)>0恒成立,则f(x)在(0,+∞)上恒为增函数. 时,由(1)知,函数
时,由(1)知,函数 在 (0,1)是增函数,在(1,2)是减函数
在 (0,1)是增函数,在(1,2)是减函数
 不大于g(x)在[1,2]的最大值
不大于g(x)在[1,2]的最大值
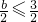 ,即b≤3时,g(x)在[1,2]为增函数,则g(x)max=g(2)=5-2b,
,即b≤3时,g(x)在[1,2]为增函数,则g(x)max=g(2)=5-2b, ,∴b≤
,∴b≤ ,满足b≤3;
,满足b≤3;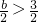 ,即b>3时,g(x)在[1,2]为减函数,则g(x)max=g(1)=2-b,
,即b>3时,g(x)在[1,2]为减函数,则g(x)max=g(1)=2-b,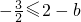 ,∴b≤
,∴b≤ ,∴3<b≤
,∴3<b≤ ,
, .
.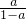 ,结合函数的定义域分类讨论,即可求得结论;
,结合函数的定义域分类讨论,即可求得结论; 时,f(x)在(0,2]的最大值为f(1)=-
时,f(x)在(0,2]的最大值为f(1)=- ,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),等价于函数f(x)在(0,2]的最大值-
,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),等价于函数f(x)在(0,2]的最大值- 不大于g(x)在[1,2]的最大值,利用配方法确定函数g(x)=x2-bx+1在[1,2]上的最大值,即可得到实数b的取值范围.
不大于g(x)在[1,2]的最大值,利用配方法确定函数g(x)=x2-bx+1在[1,2]上的最大值,即可得到实数b的取值范围.
