
设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在(1,f(1))点处的切线的方程;
(2)求函数f(x)的单调区间与极值;
(3)已知函数g(x)=f(x)+![]() 有三个互不相同的零点,求m的取值范围.
有三个互不相同的零点,求m的取值范围.
解析 (1)当m=1时,f(x)=-![]() x3+x2,f′(x)=-x2+2x,故f′(1)=1.
x3+x2,f′(x)=-x2+2x,故f′(1)=1.
所以曲线y=f(x)在点(1,f(1))处的切线斜率为1.
切线方程为3x-3y-1=0.
(2)f′(x)=-x2+2x+m2-1,令f′(x)=0,得到x=1-m或x=1+m.
因为m>0,所以1+m>1-m.
当x变化时,f(x),![]() f′(x)的变化情况如下表:
f′(x)的变化情况如下表:
| x | (-∞,1-m) | 1-m | (1-m,1+m) | 1+m | (1+m,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) |
| 极小值 |
| 极大值 |
|
f′(x)在(-∞,1-m)和(1+m,+∞)内减函数,在(1-m,1+m)内增函数.
函数f(x)在x=1+m处取得极大值f(1+m),且f(1+m)=![]() m3+m2-
m3+m2-![]() .
.
函数f(x)在x=1-m处取得极小值f(1-m),
且f(1-m)=-![]() m3+m2-
m3+m2-![]() .
.
(3)由(2)知,
函数g(x)在x=1+m处取得极大值g(1+m)=f(1+m)+![]() ,
,
且g(1+m)=![]() m3+m2.
m3+m2.
函数g(x)在x=1-m处取得极小值g(1-m)=f(1-m)+![]() ,
,
且g(1-m)=-![]() m3+m2.
m3+m2.
根据三次函数的图像与性质,函数g(x)=f(x)+![]() 有三个互不相同的零点,只需要
有三个互不相同的零点,只需要
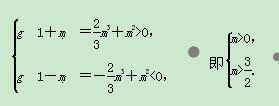 所以m的取值范围是
所以m的取值范围是![]() .
.


科目:高中数学 来源:四川省成都外国语学校2011-2012学年高一上学期期中考试数学试题 题型:044
设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)的图象上的点时,点Q(x-2a,-y)是函数y=g(x)图象上的点.
①写出函数y=g(x)的解析式;
②若x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
查看答案和解析>>
科目:高中数学 来源:山东省郓城一中2012届高三上学期寒假作业数学试卷(13) 题型:013
(理)设函数f(x)=sin(ωx+![]() )-1(ω>0)的导数
)-1(ω>0)的导数![]() (x)最大值为3,则f(x)的图像的一条对称轴的方程是
(x)最大值为3,则f(x)的图像的一条对称轴的方程是
A.x=![]()
B.x=![]()
C.x=![]()
D.x=![]()
查看答案和解析>>
科目:高中数学 来源:陕西省西安市第一中学2012届高三上学期期中考试数学理科试题 题型:022
设函数f(x)=![]() (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)=![]() ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))=![]() ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))=![]() ,f4(x)=f(f3(x))=
,f4(x)=f(f3(x))=![]() ,……根据以上事实,由归纳推理可得:当n∈N+且n≥2时,fn(x)=f(fn-1(x))=________.
,……根据以上事实,由归纳推理可得:当n∈N+且n≥2时,fn(x)=f(fn-1(x))=________.
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编(大纲版)》、数学文 大纲版 题型:044
已知函数f(x)=x3+bx2+cx+d(b、c、d∈R且都为常数)的导函数为![]() ,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
(Ⅰ)当a<2时,求F(x)的极小值;
(Ⅱ)若对任意的x∈[0,+∞),都有F(x)≥0成立,求a的取值范围并证明不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源:宁夏省银川一中2010届高三年级第一次月考测试数学试卷(理) 题型:044
设函数f(x)=ax+![]() (a,b为常数),且方程f(x)=
(a,b为常数),且方程f(x)=![]() 有两个实根为x1=-1,x2=2.
有两个实根为x1=-1,x2=2.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)的图像是一个中心对称图形,并求其对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com