
 ,②若
,②若 ,③若t≥-
,③若t≥- ,借助图象即可求得最值;
,借助图象即可求得最值; ,解得
,解得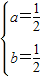 ,
, .
. ,
, ,即t≤-
,即t≤- ,fmax(x)=f(t)=
,fmax(x)=f(t)= 取不到,fmin(x)=f(t+1)=
取不到,fmin(x)=f(t+1)=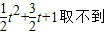 ;
; 即-
即- <t<-
<t<- ,
,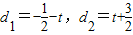 ,
,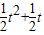 取不到,fmin(x)=f(-
取不到,fmin(x)=f(- )=-
)=- ,
,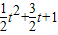 取不到,
取不到,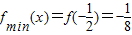 ;
; ,fmax(x)=f(t+1)=
,fmax(x)=f(t+1)=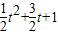 取不到,
取不到, 取不到.
取不到. 或t
或t 时,f(x)没最大值也没最小值,当-
时,f(x)没最大值也没最小值,当- <t<-
<t<- 时,最小值为-
时,最小值为- ,无最大值.
,无最大值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015届山东省高一暑假作业(一)数学试卷(解析版) 题型:解答题
已知二次函数y=f(x)(x∈R)的图像是一条开口向下且对称轴为x=3的抛物线,试比较大小:
(1)f(6)与f(4)

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com