
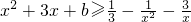 (x∈R且x≠0)恒成立,则b的最小值为
(x∈R且x≠0)恒成立,则b的最小值为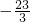


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012高考数学二轮名师精编精析(3):函数性质 题型:013
已知f(x)与g(x)是定义在R上的连续函数,如果f(x)与g(x)仅当x=0时的函数值为0,且f(x)≥g(x),那么下列情形不可能出现的是
0是f(x)的极大值,也是g(x)的极大值
0是f(x)的极小值,也是g(x)的极小值
0是f(x)的极大值,但不是g(x)的极值
0是f(x)的极小值,但不是g(x)的极值
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知af(x)+bf(![]() )=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函数,且x∈(-∞,0)时,f(x)=x2+2x,求f(x);
(4)某工厂生产一种机器的固定成本为5 000元,且每生产100部,需要增加投入2 500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入的函数为H(x)=500x-![]() x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市南开中学高三(上)11月月考数学试卷(文科)(解析版) 题型:选择题
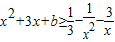 (x∈R且x≠0)恒成立,则b的最小值为( )
(x∈R且x≠0)恒成立,则b的最小值为( )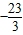



查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市南开中学高三(上)11月月考数学试卷(文科)(解析版) 题型:选择题
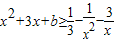 (x∈R且x≠0)恒成立,则b的最小值为( )
(x∈R且x≠0)恒成立,则b的最小值为( )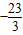
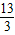

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com