
已知正态分布总体落在区间(-∞,0.3)的概率为0.5,那么相应的正态曲线φμ,σ(x)在x=________时达到最高点.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评2练习卷(解析版) 题型:解答题
设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练9练习卷(解析版) 题型:选择题
在等比数列{an}中,若a4,a8是方程x2-4x+3=0的两根,则a6的值是( ).
A.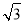 B.-
B.-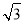 C±
C±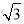 D.±3
D.±3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:填空题
若α,β∈ ,cos
,cos 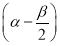 =
= ,sin
,sin 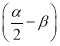 =-
=-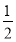 ,则cos (α+β)=________.
,则cos (α+β)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
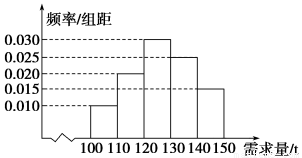
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:选择题
甲射击命中目标的概率是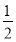 ,乙命中目标的概率是
,乙命中目标的概率是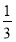 ,丙命中目标的概率是
,丙命中目标的概率是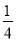 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).
A.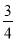 B.
B.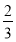 C.
C.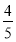 D.
D. 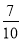
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
已知P是△ABC所在平面内一点, +2
+2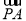 =0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( ).
=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( ).
A.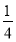 B.
B.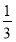 C.
C.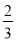 D.
D.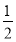
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:解答题
已知椭圆C的中心为平面直角坐标系xOy的原点,焦点在x轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆C的方程;
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的一点,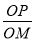 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知α,β,γ是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①a∥γ,b?β;②a∥γ,b∥β;③b∥β,a?γ.如果命题“α∩β=a,b?γ,且________,那么a∥b”为真命题,则可以在横线处填入的条件是( ).
A.①或② B.②或③ C.①或③ D.只有②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com