
 ax 3 + x2 + 2 ( a ≠ 0 ) .
ax 3 + x2 + 2 ( a ≠ 0 ) .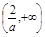 上是减函数,在
上是减函数,在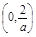 上是增函数.
上是增函数. 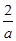 ),(0, +∞)上是增函数,在(
),(0, +∞)上是增函数,在(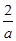 ,0)上是减函数.
,0)上是减函数. 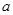 <1时,f(x)的最大值为3-
<1时,f(x)的最大值为3-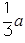 ,
,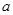 ≤2时,f(x)的最大值为
≤2时,f(x)的最大值为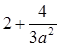 ,
,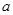 >2时,f(x)的最大值为
>2时,f(x)的最大值为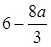 .
. 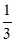 ax3+x2+2(a≠0),∴
ax3+x2+2(a≠0),∴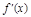 = -ax2+2x.
= -ax2+2x. 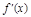 >0,即-ax2+2x>0,得0<x<
>0,即-ax2+2x>0,得0<x<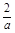 .
.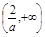 上是减函数,在
上是减函数,在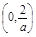 上是增函数. ………………4分
上是增函数. ………………4分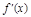 >0,即-ax2+2x>0,得x>0,或x<
>0,即-ax2+2x>0,得x>0,或x<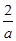 .
.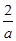 ),(0, +∞)上是增函数,在(
),(0, +∞)上是增函数,在(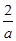 ,0)上是减函数.………………8分
,0)上是减函数.………………8分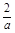 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,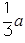 . ……………10分
. ……………10分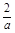 ≤2,即1≤a≤2时,f(x)在
≤2,即1≤a≤2时,f(x)在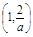 上是增函数,在
上是增函数,在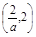 上是减函数,
上是减函数,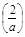 =
=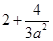 . ………12分
. ………12分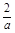 >2时,即0<
>2时,即0<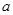 <1时,f(x)在(1,2)上是增函数,
<1时,f(x)在(1,2)上是增函数,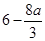 . ……………14分
. ……………14分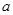 <1时,f(x)的最大值为3-
<1时,f(x)的最大值为3-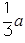 ,
,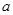 ≤2时,f(x)的最大值为
≤2时,f(x)的最大值为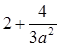 ,
,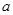 >2时,f(x)的最大值为
>2时,f(x)的最大值为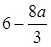 . ………………15分
. ………………15分

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源:不详 题型:解答题
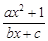 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<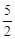 .试求函数f(x)的解析式
.试求函数f(x)的解析式查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
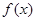 的导函数
的导函数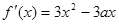 ,
,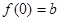 ,
,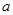 、
、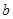 为实数。
为实数。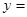
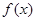 在点(
在点(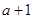 ,
,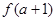 )处切线的斜率为12,求
)处切线的斜率为12,求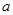 的值;
的值;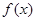 在区间[-1,1]上的最小值、最大值分别为-2、1,且
在区间[-1,1]上的最小值、最大值分别为-2、1,且 ,求函数
,求函数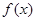 的解析式。
的解析式。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 地和
地和 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知 米.(汽车开到
米.(汽车开到 地即停止)
地即停止) 秒后,汽车到达
秒后,汽车到达 处,自行车到达
处,自行车到达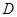 处,设
处,设 间距离为
间距离为 ,试写出
,试写出 关于
关于 的函数关系式,并求其定义域.
的函数关系式,并求其定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com