
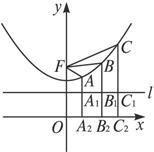
(1)求y1+y3的值;
(2)证明线段AC的垂直平分线经过某一定点,并求此点坐标.
(1)解:c=![]() =5,故F为双曲线的焦点,设准线为l,离心率为e,由题设有
=5,故F为双曲线的焦点,设准线为l,离心率为e,由题设有
2|FB|=|FA|+|FC|. ①
分别过A、B、C作x轴的垂线AA2、BB2、CC2,交l于A1、B1、C1,则由双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入①式,得2e|BB1|=e|AA1|+e|CC1|,
即2|BB1|=|AA1|+|CC1|.
于是两边均加上准线与x轴距离的2倍,有2|BB2|=|AA2|+|CC2|,
此即2×6=y1+y3,可见y1+y3=12.
(2)证明:AC的中垂线方程为
y-![]() =-
=-![]() (x-
(x-![]() ),
),
即y-6=-![]() x+
x+![]() . ②
. ②
由于A、C均在双曲线上,
所以有![]() -
-![]() =1,
=1,![]() -
-![]() =1.
=1.
相减得![]() =
=![]() .于是有
.于是有![]() =
=![]() (y1+y3)=
(y1+y3)=![]() ·12=13,
·12=13,
故②变为y=-![]() x+
x+![]() ,易知此直线过定点D(0,
,易知此直线过定点D(0,![]() ).
).
讲评:利用第二定义得焦半径,可使问题容易解决.中垂线过弦AC的中点,中点问题往往把A、C的坐标代入方程,两式相减、变形,即可解决问题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,在双曲线
如图,在双曲线| y2 |
| 12 |
| x2 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
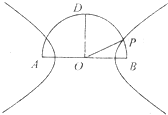 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在双曲线
如图,在双曲线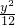 -
-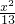 =1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:8.2 双曲线(解析版) 题型:解答题
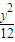 -
-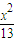 =1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.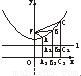
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com