
解答题:解答应写出文字说明,证明过程或演算步骤.
设P(x1,y1),Q(x2,y2)是抛物线C:y2=2px(p>0)上相异两点,且![]() ,直线PQ与x轴相交于E.
,直线PQ与x轴相交于E.
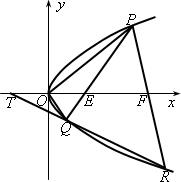
(Ⅰ)若P,Q到x轴的距离的积为4,求p的值;
(Ⅱ)若p为已知常数,在x轴上,是否存在异于E的一点F,使得直线PF与抛物线的另一交点为R,而直线RQ与x轴相交于T,且有![]() ,若存在,求出F点的坐标(用p表示),若不存在,说明理由.
,若存在,求出F点的坐标(用p表示),若不存在,说明理由.
|
解:(Ⅰ)∵ 又P、Q在抛物线上, ∴y12=2px1,y22=2px2, ∴ ∴|y1y2|=4p2, 3分 又|y1y2|=4,∴4p2=4,p=1. 4分 (Ⅱ)设E(a,0),直线PQ方程为x=my+a, 联立方程组 消去x得y2-2pmy-2pa=0, 6分 ∴y1y2=-2pa, ① 7分 设F(b,0),R(x3,y3),同理可知: y1y3=-2pb, ② 8分 由①、②可得 若 (x3-c,y3-0)=3(x2-c,y2-0), ∴y3=3y2 即 将④代入③,得 b=3a. 11分 又由(Ⅰ)知, ∴y1y2=-4p2,代入①, 得-2pa=-4p2 ∴a=2p, 13分 ∴b=6p, 故,在x轴上,存在异于E的一点F(6p,0),使得 注:若设直线PQ的方程为y=kx+b,不影响解答结果. |


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源:山西省实验中学2006-2007学年度第一学期高三年级第三次月考 数学试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:河南省信阳市商城高中2006-2007学年度高三数学单元测试、不等式二 题型:044
解答题:解答应写出文字说明,证明过程或演算步骤.
证明下列不等式:
(文)若x,y,z∈R,a,b,c∈R+,则![]() z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)
(理)若x,y,z∈R+,且x+y+z=xyz,则![]() ≥2
≥2![]()
查看答案和解析>>
科目:高中数学 来源:河南省信阳市商城高中2006-2007学年度高三数学单元测试、不等式二 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:四川省成都市名校联盟2008年高考数学冲刺预测卷(四)附答案 题型:044
解答题:解答应写出文字说明,证明过程或演算步骤.
已知函数f(x)的图像与函数![]() 的图像关于点A(0,1)对称.
的图像关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)(文)若g(x)=f(x)·x+ax,且g(x)在区间(0,2]上为减函数,求实数a的取值范围;
(理)若![]() ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:四川省成都市名校联盟2008年高考数学冲刺预测卷(四)附答案 题型:044
解答题:解答应写出文字说明,证明过程或演算步骤.
如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=![]() ,BC=
,BC=![]() .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.

(1)建立适当坐标系,求椭圆C的方程;
(2)(文)是否存在直线l与椭圆C交于M、N两点,且线段MN的中点为C,若存在,求l与直线AB的夹角,若不存在,说明理由.
(理)若点E满足![]()
![]()
![]() ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且|ME|=|NE|,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且|ME|=|NE|,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com