
科目:高中数学 来源:不详 题型:解答题
 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 表示其中合格品的个数,求
表示其中合格品的个数,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:| 分组 |  组 组 |  组 组 |  组 组 |
| 药品有效 |  |  |  |
| 药品无效 |  |  |  |
 个,抽到
个,抽到 组药品有效的概率是
组药品有效的概率是 .
. 个测试结果,问应在
个测试结果,问应在 组抽取样本多少个?
组抽取样本多少个?  ,
, ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于 %,则认为测试通过).
%,则认为测试通过).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.[0.4,1) | B.(0,0.4] | C.(0,0.6] | D.[0.6,1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立. π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,取到黑球或黄球的概率是
,取到黑球或黄球的概率是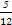 ,取到黄球或绿球的概率也是
,取到黄球或绿球的概率也是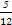 ,则取到黑球、黄球、绿球的概率分别是 .
,则取到黑球、黄球、绿球的概率分别是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com