
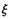 服从正态分布"(0,1),若 P(
服从正态分布"(0,1),若 P( <1) ="0.8413" 则P(-1<
<1) ="0.8413" 则P(-1<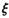 <0)=_____.
<0)=_____.科目:高中数学 来源:不详 题型:解答题
 ,外语考核合格的概率是
,外语考核合格的概率是 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
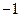 分,一名观众随意连线,将他的得分记作ξ.
分,一名观众随意连线,将他的得分记作ξ.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
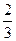 .(1)求连续射击5次,恰有3次击中目标的概率;
.(1)求连续射击5次,恰有3次击中目标的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
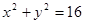 内的次数
内的次数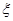 的均值为________
的均值为________查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与
与 的随机变量
的随机变量 的观测值是
的观测值是 ,说法正确的是 ( )
,说法正确的是 ( )A. 越接近于0,“ 越接近于0,“ 与 与 无关”程度越小 无关”程度越小 | B. 越大,“ 越大,“ 与 与 无关”程度越大 无关”程度越大 |
C. 越大,“ 越大,“ 与 与 有关系”可信程度越小 有关系”可信程度越小 | D. 越小,“ 越小,“ 与 与 有关系”可信度越小 有关系”可信度越小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com