
分析 利用二倍角公式及诱导公式求得tan2(α+$\frac{π}{4}$)=tan(2α+π)=tan2α,sin(2α-π)=-sin2α,根据α的取值范围,及tan2α<0,求得2α的取值范围,根据同角三角关系即可求得sin2α的值,由诱导公式sin(2α-π)=-sin2α,即可求得sin(2α-π)的值.
解答 解:tan2(α+$\frac{π}{4}$)=$\frac{2tan(α+\frac{π}{4})}{1-ta{n}^{2}(α+\frac{π}{4})}$=$\frac{2×(-\frac{1}{7})}{1-(\frac{1}{7})^{2}}$=-$\frac{7}{24}$,
∴tan(2α+π)=tan2α,
∴tan2α=-$\frac{7}{24}$,
α∈($\frac{π}{2}$,π),2α∈(π,2π),
∵tan2α<0,
∴2α∈($\frac{3π}{2}$,2π),
由$\left\{\begin{array}{l}{tan2α=\frac{sin2α}{cos2α}}\\{si{n}^{2}2α+co{s}^{2}2α=1}\end{array}\right.$,解得:sin2α=-$\frac{7}{25}$,
sin(2α-π)=-sin2α=$\frac{7}{25}$,
故答案为:$\frac{7}{25}$.
点评 本题考查三角恒等变形,考查二倍角公式、诱导公式及同角的三角关系,考查了计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
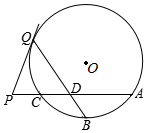 如图,A,B,C为圆O上三点,点B平分弧$\widehat{AC}$,点P为AC延长线上一点,PQ是圆O的切线,切点为Q,BQ与AC相交于点D.
如图,A,B,C为圆O上三点,点B平分弧$\widehat{AC}$,点P为AC延长线上一点,PQ是圆O的切线,切点为Q,BQ与AC相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
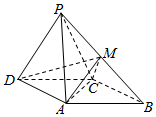 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
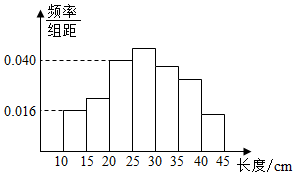 从一条生产线上每隔30min取一件产品,共取了n件,测得它们的长度(单位:cm)后,画出其频率分布直方图如图所示,若长度在[20,25)cm内的频数为40,则长度在[10,15)cm内的产品共有16件.
从一条生产线上每隔30min取一件产品,共取了n件,测得它们的长度(单位:cm)后,画出其频率分布直方图如图所示,若长度在[20,25)cm内的频数为40,则长度在[10,15)cm内的产品共有16件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com