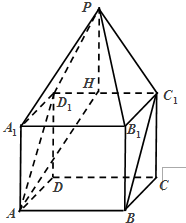
分析:(Ⅰ)取D1C1的中点H,连接PH,AH.可以证得四边形PA1AH为平行四边形,即PA1∥AH,进而由线面平行的判定定理可得PA1∥平面ABC1D1.
(Ⅱ)由PA1∥AH,可得直线PA1与平面ADD1A1所成角等于直线AH与平面ADD1A1所成角,即∠HAD1就是直线AH与平面ADD1A1所成角,解Rt△HAD1,可得直线PA1与ADD1A1所成角的正切值.
解答:证明:
(Ⅰ)取D
1C
1的中点H,连接PH,AH.
∵
PC1=PD1=,D
1C
1=1,P∈平面DCC
1D
1,
∴
PH⊥D1C1,D1H=,
∴
PH==1,(2分)
∴PH∥D
1D∥A
1A,PH=A
1A,
∴四边形PA
1AH为平行四边形,
∴PA
1∥AH,(4分)
又AH?平面ABC
1D
1,PA
1?平面ABC
1D
1,
∴PA
1∥平面ABC
1D
1. (7分)
(Ⅱ)∵PA
1∥AH,
∴直线PA
1与平面ADD
1A
1所成角等于直线AH与平面ADD
1A
1所成角.
正方体ABCD-A
1B
1C
1D
1中,显然HD
1⊥平面ADD
1A
1,
∴∠HAD
1就是直线AH与平面ADD
1A
1所成角. (10分)
在Rt△HAD
1中,
D1H=,
AD1=,
tan∠HAD1==∴直线PA
1与平面ADD
1A
1所成角的正切值为
. (14分)
点评:本题考查的知识点是直线与平面平行的判定,直线与平面所成的角,(I)的关键是证得四边形PA1AH为平行四边形,(II)的关键是分析出∠HAD1就是直线AH与平面ADD1A1所成角.

 如图,ABCD-A1B1C1D1是棱长为1的正方体,四棱锥P-A1B1C1D1中,P∈平面DCC1D1,PC1=PD1=
如图,ABCD-A1B1C1D1是棱长为1的正方体,四棱锥P-A1B1C1D1中,P∈平面DCC1D1,PC1=PD1= (Ⅰ)取D1C1的中点H,连接PH,AH.
(Ⅰ)取D1C1的中点H,连接PH,AH.

 备战中考寒假系列答案
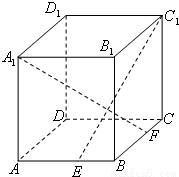
备战中考寒假系列答案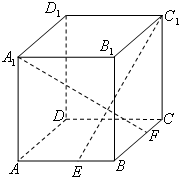 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是