练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．设等比数列{an}的前n项和为Sn，若a3=3，且a2016+a2017=0，则S101等于（　　）
    A．3B．303C．-3D．-303

    分析 由等比数列的通项公式列出方程组，求出首项和公比，由此能求出S101．

    解答 解：∵等比数列{an}的前n项和为Sn，a3=3，且a2016+a2017=0，
    ∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=3}\\{{a}_{1}{q}^{2015}（1+q）=0}\end{array}$，解得a1=3，q=-1，
    ∴S101=$\frac{{a}_{1}（1-{q}^{101}）}{1-q}$=$\frac{3（1-（-1）^{101}）}{1-（-1）}$=$\frac{3×2}{2}$=3．
    故选：A．

    点评 本题考查等比数列的第101项的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

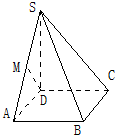    4．如图，四棱锥S-ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SD=1，SB=$\sqrt{3}$．
    （I）求证BC⊥SC；　
    （Ⅱ）求平面SBC与平面ABCD所成二面角的大小；
    （Ⅲ）设棱SA的中点为M，求异面直线DM与SB所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知x、y满足约束条件$\left\{\begin{array}{l}{x-y≥1}\\{2x-y+1≤0}\end{array}\right.$，且目标函数z=mx-ny（m＞0，n＜0）的最大值为-6，则$\frac{n}{m-1}$的取值范围是（　　）
    A．[-2，0]∪[$\frac{1}{2}$，+∞）B．[2，+∞）C．（-∞，0）∪（2，+∞）D．（-∞，0）∪[$\frac{1}{2}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．“若x2=1，则x=1”的否命题为（　　）
    A．若x2≠1，则x=1B．若x2=1，则x≠1C．若x2≠1，则x≠1D．若x≠1，则x2≠1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知A={y|y=x+1}，B=（x，y）|x2+y2=1}，则集合A∩B中元素的个数为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若函数f（x）=$\frac{1}{3}$x3-（a+$\frac{1}{2}$）x2+（a2+a）x-$\frac{1}{2}$a2+$\frac{1}{2}$有两个以上的零点，则a的取值范围是（　　）
    A．（-2，-1）B．（-∞，-2）∪（-1，+∞）C．$（-\root{3}{{\frac{3}{2}}}，-1）$D．$（-∞，-\root{3}{{\frac{3}{2}}}）∪（-1，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2$\sqrt{3}$，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为sin$\frac{17π}{3}$，则$\overrightarrow{b}$•（2$\overrightarrow{a}$-$\overrightarrow{b}$）等于（　　）
    A．2B．-1C．-6D．-18

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知函数f（x）=$\left\{\begin{array}{l}{x^2}+2x（{x≥0}）\\ g（x）（{x＜0}）\end{array}$为奇函数，则g（-1）=-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在平面直角坐标系xOy中，已知曲线C1：$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.（θ为参数）$，以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ（2cosθ-sinθ）=6．
    （1）将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的$\sqrt{3}$、2倍后得到曲线C2；试写出直线l的直角坐标方程和曲线C2的参数方程；
    （2）在曲线C2上求一点P，使点P到直线l的距离最大，并求出此最大值．

    查看答案和解析>>

    同步练习册答案