
下列函数中,既是偶函数又在区间 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
D
解析试题分析:根据函数奇偶性以及单调性的概念,那么可知
选项A中,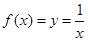 ,定义域关于原点对称,且有
,定义域关于原点对称,且有 是奇函数。不符合题意。
是奇函数。不符合题意。
而选项B中,由于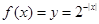 ,
,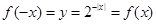 ,因此是偶函数, 当时利用复合函数单调性的判定可知,当x>0时,外层函数递增,内层函数递减,则复合函数是递减的。错误。
,因此是偶函数, 当时利用复合函数单调性的判定可知,当x>0时,外层函数递增,内层函数递减,则复合函数是递减的。错误。
选项C中,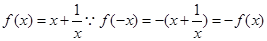 是奇函数, 不符合。
是奇函数, 不符合。
选项D,作为二次函数,开口向上,对称轴为y轴,显然是偶函数,同时也是定义域内增函数,因此成立。故选D.
考点:本试题考查了函数的奇偶性和函数单调性的概念。
点评:对于函数的奇偶性的判定,一般要抓住两点:定义域是否关于原点对称,同时解析式f(-x)与f(x)的和为零,还是差为零来得到判定,而单调性的问题,主要是熟悉常见的基本初等函数的单调性,结合性质来判定,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com