
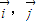 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设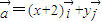 ,
,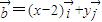 ,且满足
,且满足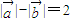
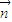 =(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,
=(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,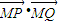 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围.
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围.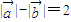 ”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;
”可以看成是动点到两定点的距离之差为2,联想双曲线的定义解决“点P(x,y)的轨迹C”问题,即点P(x,y)的轨迹是以(-2,0),(2,0)为焦点,2a=2的双曲线,从而解决问题;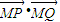 值,从而解决问题.
值,从而解决问题.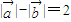 ”知:动点到两定点的距离之差为2,是双曲线,
”知:动点到两定点的距离之差为2,是双曲线,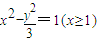 ,((4分)+(1分)定义域)
,((4分)+(1分)定义域)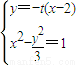 得(t2-3)x2-4t2x+4t2+3=0(1分)
得(t2-3)x2-4t2x+4t2+3=0(1分)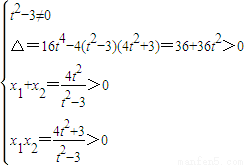 (只计算△=36+36t2>01分)
(只计算△=36+36t2>01分)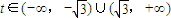 ((1分)
((1分)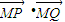 =(x1+1)(x2+1)+y1y2(1分)
=(x1+1)(x2+1)+y1y2(1分)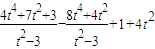 =0(2分).
=0(2分).

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,| MF |
| FB |
| B1F |
| OF |
| A1F |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省扬州市高二(上)期末数学试卷(解析版) 题型:解答题
 ),求直线l的斜率k的取值范围.
),求直线l的斜率k的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高二(下)3月月考数学试卷(理科)(解析版) 题型:解答题
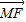 =λ
=λ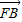 (λ>0)
(λ>0)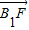 |,|
|,|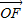 |,2|
|,2|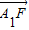 |成等差数列求λ的值
|成等差数列求λ的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com