
已知数列![]() 是等比数列,
是等比数列,![]() 为其前
为其前![]() 项和.
项和.
(1)若![]() ,
,![]() ,
,![]() 成等差数列,证明
成等差数列,证明![]() ,
,![]() ,
,![]() 也成等差数列;
也成等差数列;
(2)设![]() ,
,![]() ,
,![]() ,若数列
,若数列![]() 是单调递减数列,求实数
是单调递减数列,求实数![]() 的取值范围.
的取值范围.
(1)设数列![]() 的公比为
的公比为![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,且
,且![]() .
.
所以![]() ,
,
因为![]() ,所以
,所以![]() . …………………………………………4分
. …………………………………………4分
所以![]() ,即
,即![]() .
.
所以![]() 也成等差数列. ………………………………………………6分
也成等差数列. ………………………………………………6分
(2)因为![]() ,
,![]() ,
,
所以![]() ,……………………①
,……………………①
![]() ,……………………②
,……………………②
由②![]() ①,得
①,得![]() ,所以
,所以![]() ,代入①,得
,代入①,得![]() .
.
所以![]() , ………………………………………………………8分
, ………………………………………………………8分
又因为![]() ,所以
,所以![]() ,
,
由题意可知对任意![]() ,数列
,数列![]() 单调递减,
单调递减,
所以![]() ,即
,即![]()
![]() ,
,
即![]() 对任意
对任意![]() 恒成立, ………………………………10分
恒成立, ………………………………10分
当![]() 是奇数时,
是奇数时,![]() ,当
,当![]() ,
,![]() 取得最大值-1,
取得最大值-1,
所以![]() ; ………………………………………………………………12分
; ………………………………………………………………12分
当![]() 是偶数时,
是偶数时,![]() ,当
,当![]() ,
,![]() 取得最小值
取得最小值![]() ,
,
所以![]()
![]() .
.
综上可知,![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .…………14分
.…………14分


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:2012-2013学年广东省深圳市高三12月月考文科数学试卷(解析版) 题型:选择题
已知数列 是等比数列,且
是等比数列,且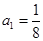 ,
, ,则
,则 的公比
的公比 为( )
为( )
A.-2 B.- C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌市高三第二次模拟测试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)等差数列{an}中,公差d≠0,已知数列 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.
(1)求数列{kn}的通项;
(2)若a1=9,设bn=  +
+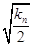 ,Sn=b12+b22+b32+…+
bn2, Tn=
,Sn=b12+b22+b32+…+
bn2, Tn= 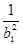 +
+ +
+ +…+
+…+ ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com