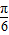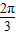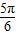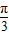已知向量
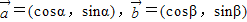
,并且满足关系:
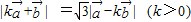
,则
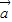
与
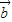
的夹角最大值为( )
A.
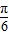
B.
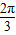
C.
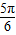
D.
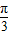
【答案】
分析:通过
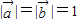
且
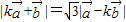
,两边平方化简可得化简可得数量积的表达式,设
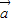
与
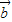
夹角为θ,根据向量的夹角公式可得
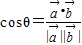
,得到关于k的表达式,利用二次函数的性质可求.
解答:解:由题意,
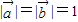
且
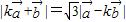
,
所以

,
化简可得
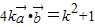
,
∴
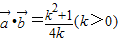
;
设
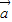
与
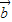
夹角为θ,
则

=
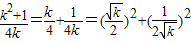
=
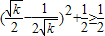
因此,当且仅当
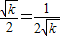
即k=1时,cosθ有最小值为

,
此时,向量

与
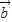
的夹角有最大值为60°.
点评:本题考查了平面向量的数量积的性质:
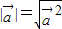
,考查了向量的夹角公式与二次函数的综合应用.
练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年辽宁省高三上学期期中考试理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年辽宁省铁岭市高级中学高三(上)期中数学试卷(文科)(解析版)
题型:选择题
已知向量

,并且满足关系:
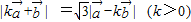
,则
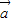
与
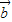
的夹角最大值为( )
A.
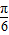
B.
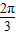
C.
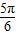
D.
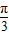
查看答案和解析>>
科目:高中数学
来源:2008-2009学年重庆一中高一(下)5月月考数学试卷(解析版)
题型:选择题
已知向量

,并且满足关系:

,则

与

的夹角最大值为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2013年吉林省吉林一中高考数学模拟试卷(一)(解析版)
题型:选择题
已知向量
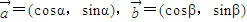
,并且满足关系:

,则
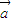
与
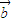
的夹角最大值为( )
A.
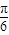
B.
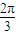
C.
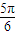
D.
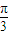
查看答案和解析>>

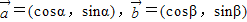 ,并且满足关系:
,并且满足关系: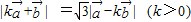 ,则
,则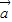 与
与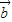 的夹角最大值为( )
的夹角最大值为( )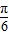
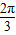
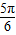
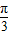
 ,并且满足关系:
,并且满足关系: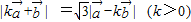 ,则
,则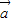 与
与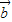 的夹角最大值为( )
的夹角最大值为( )