
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
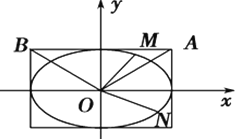
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为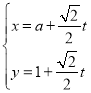 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,已知asinB=bsin2A.
(1)求角A;
(2)若a=5,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4公里,丙、甲两地距离是丙、乙两地距离的![]() 倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com