
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为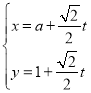 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
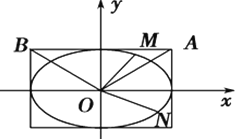
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.
(1)求选出的4名选手中恰好有一名女教师的选派方法数;
(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低雾霾等恶劣气候对居民的影响,某公司研发了一种新型防雾霾产品.每一台新产品在进入市场前都必须进行两种不同的检测,只有两种检测都合格才能进行销售,否则不能销售.已知该新型防雾霾产品第一种检测不合格的概率为![]() ,第二种检测不合格的概率为
,第二种检测不合格的概率为![]() ,两种检测是否合格相互独立.
,两种检测是否合格相互独立.
(1)求每台新型防雾霾产品不能销售的概率;
(2)如果产品可以销售,则每台产品可获利40元;如果产品不能销售,则每台产品亏损80元(即获利![]() 元).现有该新型防雾霾产品3台,随机变量
元).现有该新型防雾霾产品3台,随机变量![]() 表示这3台产品的获利,求
表示这3台产品的获利,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 在区间
在区间![]() 上是增函数.
上是增函数.
(1)求实数![]() 的值组成的集合
的值组成的集合![]() ;
;
(2)设关于![]() 的方程
的方程![]() 的两个非零实根为
的两个非零实根为![]() 、
、![]() .试问:是否存在实数
.试问:是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com