
【题目】【2018届安徽省合肥市高三第一次教学质量检测】一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在![]() 内的顾客中,随机抽取了180人,调查结果如表:
内的顾客中,随机抽取了180人,调查结果如表:

(1)为推广移动支付,商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物,试根据上述数据估计,该商场当天应准备多少个环保购物袋?
(2)某机构从被调查的使用移动支付的顾客中,按分层抽样的方式抽取7人作跟踪调查,并给其中2人赠送额外礼品,求获得额外礼品的2人年龄都在![]() 内的概率.
内的概率.
【答案】(1)7000个;(2) ![]() .
.
【解析】试题分析:
(1)由表可知,该商场使用移动支付的顾客的比例为![]() ,据此估计该商场要准备环保购物袋
,据此估计该商场要准备环保购物袋![]() 个;
个;
(2)按年龄分层抽样时,抽样比例为![]() ,所以应从
,所以应从![]() 内抽取3人,从
内抽取3人,从![]() 内抽取2人,从
内抽取2人,从![]() 内抽取1人,从
内抽取1人,从![]() 内抽取1人.列出所有可能的基本事件,结合古典概型计算公式可得获得额外礼品的2人年龄都在
内抽取1人.列出所有可能的基本事件,结合古典概型计算公式可得获得额外礼品的2人年龄都在![]() 内的概率为
内的概率为![]() .
.
试题解析:
(1)由表可知,该商场使用移动支付的顾客的比例为![]() ,
,
若当天该商场有12000人购物,则估计该商场要准备环保购物袋![]() 个;
个;
(2)按年龄分层抽样时,抽样比例为![]() ,所以应从
,所以应从![]() 内抽取3人,从
内抽取3人,从![]() 内抽取2人,从
内抽取2人,从![]() 内抽取1人,从
内抽取1人,从![]() 内抽取1人.
内抽取1人.
记选出年龄在![]() 的3人为
的3人为![]() ,其他4人为
,其他4人为![]() ,7个人中选取2 人赠送额外礼品,有以下情况:
,7个人中选取2 人赠送额外礼品,有以下情况:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
共有21种不同的情况,其中获得额外礼品的2人都在![]() 的情况有3种,
的情况有3种,
所以,获得额外礼品的2人年龄都在![]() 内的概率为
内的概率为![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
①当x>10时,![]() ; ②当x∈R,x2+x=0有解
; ②当x∈R,x2+x=0有解
③当a∈R关于x的方程x2+a=0在实数集内有解; ④当sinα>sinβ时,α>β( )
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点,欲过点
的中点,欲过点![]() 作一截面与平面
作一截面与平面![]() 平行.
平行.
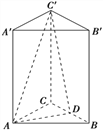
(I)问应当怎样画线,并说明理由;
(II)求所作截面与平面![]() 将三棱柱分成的三部分的体积之比.
将三棱柱分成的三部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,用简单随机抽样方法调查了125人,其中女性70人,男性55人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
(3)在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座,讲座结束后再从这6人中抽取2人作反馈交流,求参加交流的恰好为2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
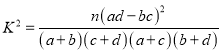
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com