Question

（1）（坐标系与参数方程选做题）
在直角坐标系xoy中，以原点为极点，x轴为非负半轴为极轴建立极坐标系，已知圆C与直线l的方程分别为：ρ=2sinθ，（t为参数）．若圆C被直线l平分，则实数x₀的值为________．
（2）（不等式选做题）
若关于x的不等式|xx-m|＜2成立的充分不必要条件是2≤x≤3，则实数m的取值范围是________．

Answer 1

解：（1）．圆的极坐标方程为：ρ=2sinθ，即：ρ²=2ρsinθ，
化为直角坐标方程为x²+y²=2y，即为x²+（y-1）²=1．
表示以C（0，1）为圆心，半径为1 的圆．
线l的方程化为x-x₀=y，
若圆C被直线l平分，只需直线经过圆的圆心，所以x₀=-1
故答案为：-1
（2）．因为|x-m|＜2，即-2＜x-m＜2，即m-2＜x＜m+2；
由已知不等式|x-m|＜1成立的充分非必要条件是2≤x≤3
即2≤x≤3是|x-m|＜1解集的子集，即
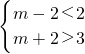
解得实数m的取值范围是（1，4）
故答案为：（1）-1；（2）（1，4）．
分析：（1）．若圆C被直线l平分，只需直线经过圆的圆心．化圆、直线方程为普通方程，求出圆心坐标，代入直线方程求解．
（2）．首先分析题目已知不等式|x-m|＜1成立的充分不必要条件是2≤x≤3，求m的取值范围，故可以考虑先根据绝对值不等式的解法解出|x-m|＜1含有参数m的解，又因为充分不必要条件，是条件可以推出结论，结论推不出条件，即2≤x≤3是|x-m|＜1解集的子集，建立关于m的不等关系，从而解决问题．
点评：（1）．本小题以曲线参数方程出发，考查了极坐标方程、普通方程间的互化，直线和圆的位置关系．
（2）．主要考查绝对值不等式的解法问题，其中涉及到必要条件、充分条件的知识，题目的计算量小，主要考查的是概念性问题，属于基础题目．