
已知函数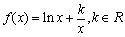
(1)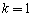 时函数
时函数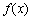 的单调性;
的单调性;
(2)若 恒成立,求实数
恒成立,求实数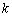 的取值范围;
的取值范围;
(3)设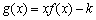 ,若对任意的两个实数
,若对任意的两个实数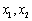 满足
满足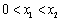 ,总存在
,总存在 ,使得
,使得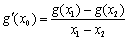 成立,证明:
成立,证明: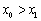
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
有6人入住宾馆中的6个房间,其中的房号301与302对门,303与304对门,305与306对门,若每人随机地拿了这6个房间中的一把钥匙,则其中的甲、乙两人恰好对门的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
将正偶数按下表排成4列:
第1列 第2列 第3列 第4列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
… … 28 26
则2 004在 ( )
(A)第251行,第1列 (B)第251行,第2列
(C)第250行,第2列 (D)第250行,第4列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com