
已知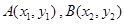 是
是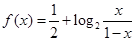 的图象上任意两点,设点
的图象上任意两点,设点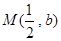 ,且
,且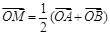 ,若
,若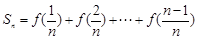 ,其中
,其中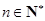 ,且
,且 .
.
(1)求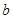 的值;
的值;
(2)求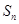 ;
;
(3)数列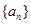 中
中 ,当
,当 时,
时,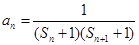 ,设数列
,设数列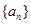 的前
的前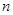 项和为
项和为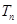 ,求
,求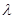 的取值范围使
的取值范围使 对一切
对一切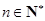 都成立.
都成立.
(1)由 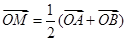 ,得点
,得点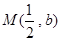 是
是 的中点,
的中点,
则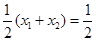 , 故
, 故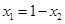 ,
,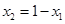 ,
,
所以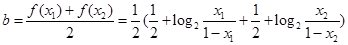
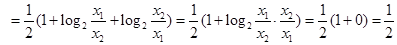
(2)由(1)知当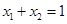 时,
时,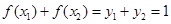 .
.
又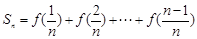 ,∴
,∴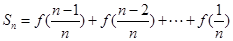 ,
,
∴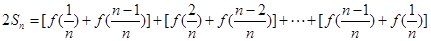
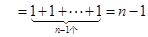
 (
(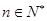 ,且
,且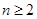 ).
).
(3)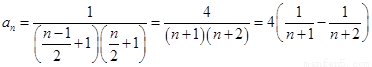 ,
,
故当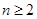 时
时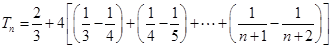
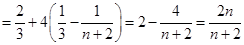 ,故由
,故由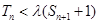 得
得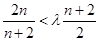 ,
,
即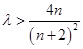 ,只要
,只要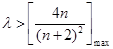 ,
,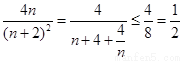 ,
,
故当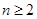 时,
时,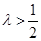 ;当
;当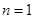 是
是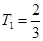 ,
,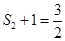 ,由
,由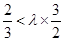 得
得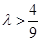 ,而
,而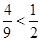 .
.
故当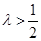 时可以对一切
时可以对一切 不等式
不等式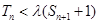 都成立.
都成立.
【解析】(1)
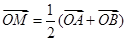 ,得点
,得点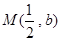 是
是 的中点,
的中点,
则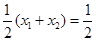 , 故
, 故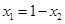 ,
,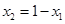 .这是解本小题的关键.
.这是解本小题的关键.
(2) 由(1)知当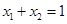 时,
时,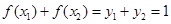 .
.
又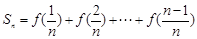 ,下面采用倒序相加的方法求和即可.
,下面采用倒序相加的方法求和即可.
(3) 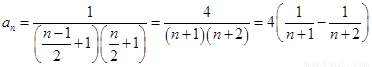
所以采用裂项求和的方法求解即可.
【点评】数列是以正整数为自变量的函数,从函数入手设计数列试题是自然的.本题从函数图象的对称性出发构造了一个函数值的数列,再从这些已经解决的问题入手构造了一个裂项求和问题和一个不等式恒成立问题,试题设计逐步深入.解答数列求和时要注意起首项是不是可以融入整体,实际上本题得到的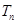 对
对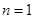 也成立
也成立


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源:2012-2013学年河北省高三第一次调研考试理科数学试卷(解析版) 题型:解答题
对于函数 ,若存在
,若存在 ,使
,使 ,则称
,则称 是
是 的一
的一
个"不动点".已知二次函数
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)对任意实数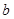 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求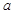 的取值范围;
的取值范围;
(3)在(2)的条件下,若 的图象上
的图象上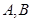 两点的横坐标是
两点的横坐标是 的不动点,
的不动点,
且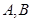 两点关于直线
两点关于直线 对称,求
对称,求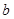 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分) 定义:若函数![]() 对于其定义域内的某一数
对于其定义域内的某一数![]() ,有
,有![]() ,则称
,则称![]() 是
是![]() 的一个不动点. 已知函数
的一个不动点. 已知函数![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意的实数b,函数![]() 恒有两个不动点,求a的取值范围;
恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若![]() 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数![]() 的不动点,且A、B的中点C在函数
的不动点,且A、B的中点C在函数![]() 的图象上,求b的最小值.
的图象上,求b的最小值.
(参考公式:![]() 的中点坐标为
的中点坐标为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
定义:若函数![]() 对于其定义域内的某一数
对于其定义域内的某一数![]() ,有
,有![]() ,则称
,则称![]() 是
是![]() 的一个不动点. 已知函数
的一个不动点. 已知函数![]() .
.
(1) 当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2) 若对任意的实数b,函数![]() 恒有两个不动点,求a的取值范围;
恒有两个不动点,求a的取值范围;
(3) 在(2)的条件下,若![]() 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数![]() 的不动点,且A、B的中点C在函数
的不动点,且A、B的中点C在函数![]() 的图象上,求b的最小值.
的图象上,求b的最小值.
(参考公式:![]() 的中点坐标为
的中点坐标为![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com