
 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.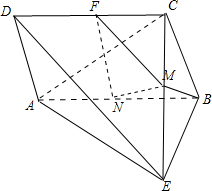 解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;
解:(Ⅰ)∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE,即AE⊥BM;| 5 |
| 3 |
| AE |
| AC |
| ||
|
| ||
| 5 |
| ||
| 5 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
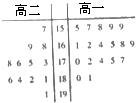 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 5 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 20000 |
| π |
| 20000 |
| 2π |
| 20000 |
| 3π |
| 20000 |
| 10000π |
| 20000 |
| A、0.99818 |
| B、0.9999 |
| C、1.0001 |
| D、2.0002 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com