
����Ŀ���ס��ҡ�������Ͷ����ˮƽ���Ƚ��ȶ��������˸��Զ����ؽ���һ��Ͷ�����ԣ����Ͷ�ж��Ҳ�Ͷ�еĸ���Ϊ ![]() ����Ͷ�ж�����Ͷ�еĸ���Ϊ
����Ͷ�ж�����Ͷ�еĸ���Ϊ ![]() ���ס������˶�Ͷ�еĸ���Ϊ
���ס������˶�Ͷ�еĸ���Ϊ ![]() ��
��
��1���ֱ���ס��ҡ������˸���Ͷ��һ��Ͷ�еĸ��ʣ�
��2����������Ͷ��5�Σ���ǡ��2��Ͷ�еĸ��ʣ�
��3����������Ͷ��3�Σ�ÿ��Ͷ����Ͷ�е�2�֣�δͶ�е�0�֣���3��Ͷ���У�����2������Ͷ�У�������1��δͶ�У�������1�֣���3��ȫͶ�У�������3�֣��Ǧ�Ϊ������Ͷ��3�κ���ܵ÷֣���εķֲ��к�������
���𰸡�
��1���⣺�Ǽס��ҡ������˸��Զ����ؽ���һ��Ͷ������Ͷ�е��¼�����ΪA��B��C�������������У�
![]() =
= ![]() ��
�� ![]() =
= ![]() ��P��AC��=
��P��AC��= ![]() ����P��A��[1��P��B��]=
����P��A��[1��P��B��]= ![]() ���٣�P��B��[1��P��C��]=
���٣�P��B��[1��P��C��]= ![]() ����P��A��P��C��=
����P��A��P��C��= ![]() ���ۣ�
���ۣ�
�ɢ٢۵�P��B��=1�� ![]() P��C��������ڵ�27P��C��]2��51P��C��+22=0��
P��C��������ڵ�27P��C��]2��51P��C��+22=0��
���P��C��= ![]() ��P��C��=
��P��C��= ![]() ����ȥ������P��C��=
����ȥ������P��C��= ![]() �ֱ����ڢۿɵ�P��A��=
�ֱ����ڢۿɵ�P��A��= ![]() ��P��B��=
��P��B��= ![]() ��
��
�ʼס��ҡ������˸���Ͷ��һ��Ͷ�еĸ��ʷֱ��� ![]() ��
�� ![]() ��
�� ![]()
��2���⣺������Ͷ��5�Σ�ǡ��2��Ͷ�еĸ���Ϊ ![]()
��3���⣺�ο���ȡ��ֵΪ0��2��4��5��9������ã� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��εķֲ���Ϊ��
�� | 0 | 2 | 4 | 5 | 9 |
p |
|
|
|
|
|
�������ΪE��=0+ ![]() +5��
+5�� ![]() +9��
+9�� ![]() =
= ![]()
����������1���Ǽס��ҡ������˸��Զ����ؽ���һ��Ͷ������Ͷ�е��¼�����ΪA��B��C�������������У� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��P��AC��=
��P��AC��= ![]() ��������ɵó�����2��������Ͷ��5�Σ�ǡ��2��Ͷ�еĸ���Ϊ
��������ɵó�����2��������Ͷ��5�Σ�ǡ��2��Ͷ�еĸ���Ϊ ![]() ����3���ο���ȡ��ֵΪ0��2��4��5��9������ã�
����3���ο���ȡ��ֵΪ0��2��4��5��9������ã� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���ɵæεķֲ��м�����ѧ������
���ɵæεķֲ��м�����ѧ������
�����㾫����������Ҫ��������ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ�������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮


 ��������ѧ����ϵ�д�
��������ѧ����ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}���� ![]() =1������d�ʣ���1��0�������ҽ���n=9ʱ������{an}��ǰn���Snȡ�����ֵ�������������a1��ȡֵ��Χ�ǣ� ��
=1������d�ʣ���1��0�������ҽ���n=9ʱ������{an}��ǰn���Snȡ�����ֵ�������������a1��ȡֵ��Χ�ǣ� ��
A.�� ![]() ��
�� ![]() ��
��
B.[ ![]() ��
�� ![]() ]
]
C.�� ![]() ��
�� ![]() ��
��
D.[ ![]() ��
�� ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c���� ![]() ��
��
��1�����A��ֵ��
��2������B= ![]() ��BC��������AM=
��BC��������AM= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij����ij��ũ��Ʒ�������x����λ���֣��Լ۸�y����λ��ǧԪ/�֣�������z��Ӱ�죬�Խ������ũ��Ʒ��������ͼ۸�ͳ�������
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
������y����x�����Իع鷽�� ![]() ��
��
������ÿ�ָ�ũ��Ʒ�ijɱ�Ϊ2ǧԪ�������ũ��Ʒ��ȫ��������Ԥ������Ϊ����ʱ��������zȡ�����ֵ����������λС����
�ο���ʽ�� ![]() =
= 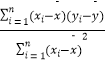 =
= 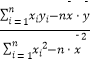 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{ an}��һ���������0�ĵȲ����У�������a3a6=55��a2+a7=16��
��1��������{ an}��ͨ�ʽ��
��2��������{bn}���� ![]() +��+
+��+ ![]() =an ��n��N* �� ������{bn}��ǰn���Sn ��
=an ��n��N* �� ������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������������10��Ԫ��ÿ��ʹ�õı��շѡ���·�ѡ�������ԼΪ0.9��Ԫ����ά�ѵ�һ����0.2��Ԫ���Ժ��������0.2��Ԫ������������ʹ�ö�����ʱ������ƽ���������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в���ʽ����ȷ���ǣ� ��
A.sin ![]() �У�sin
��sin ![]() ��
��
B.tan ![]() ��tan����
��tan���� ![]() ��
��
C.sin���� ![]() ����sin����
����sin���� ![]() ��
��
D.cos���� ![]() ����cos����
����cos���� ![]() ��
�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC�ķ���Ϊ��x��1��2+��y��2��2=4�� ���������M��3��1����ԲC�����߷��̣�
�����ж�ֱ��ax��y+3=0��ԲC��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��λ��A������Ϣ���Ļ�Ϥ�����������������40�����B����һ���洬���գ���ԭ�صȴ�Ӫ�ȣ���Ϣ������������Ϣ��֪������ƫ��30�㡢���20�����C�����Ҵ������Ҵ�����ƫ���ȵķ�����ֱ��CBǰ��B����Ԯ����cos��=��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com