
【题目】已知{ an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{ an}的通项公式;
(2)若数列{bn}满足 ![]() +…+
+…+ ![]() =an (n∈N* ) 求数列{bn}的前n项和Sn .
=an (n∈N* ) 求数列{bn}的前n项和Sn .
【答案】
(1)解:∵数列{ an}是等差数列,且a2+a7=16,
∴a3+a6=16,又∵a3a6=55,且数列{ an}的公差大于0,
∴a3=5,a6=11,则其公差d= ![]() =2,
=2,
∴an=a3+(n﹣3)2=5+2n﹣6=2n﹣1;
(2)解:由题意得b1=2a1=2.
当n≥2时,an﹣an﹣1=( ![]() +…+
+…+ ![]() )﹣(
)﹣( ![]() +…+
+…+ ![]() )
)
= ![]() ,
,
∴ ![]() ,则
,则 ![]() .
.
∴数列{bn}是以2为首项,以2为公比的等比数列,其前n项和Sn= ![]()
【解析】(1)由已知列式求得等差数列的公差,代入等差数列的通项公式求得数列{ an}的通项公式;(2)由 ![]() +…+
+…+ ![]() =an 求得b1及bn , 可得数列{bn}是以2为首项,以2为公比的等比数列,则数列{bn}的前n项和Sn可求.
=an 求得b1及bn , 可得数列{bn}是以2为首项,以2为公比的等比数列,则数列{bn}的前n项和Sn可求.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系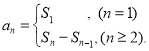 .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}为等差数列,a1=2,{an}的前n项和为Sn , 数列{bn}为等比数列,且a1b1+a2b2+a3b3+…+anbn=(n﹣1)2n+2+4对任意的n∈N*恒成立.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在非零整数λ,使不等式sin ![]() <
< ![]() 对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
(3)各项均为正整数的无穷等差数列{cn},满足c39=a1007 , 且存在正整数k,使c1 , c39 , ck成等比数列,若数列{cn}的公差为d,求d的所有可能取值之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,下列结论正确的个数为( ) ①若
,下列结论正确的个数为( ) ①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() ;
;
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3;
,则k=﹣3;
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为30°;
的夹角为30°;
④已知向量 ![]() ,且
,且 ![]() 与
与 ![]() 的夹角为锐角,则实数λ的取值范围是
的夹角为锐角,则实数λ的取值范围是 ![]() .
.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足Sn= ![]() an﹣n(t>0且t≠1,n∈N*)
an﹣n(t>0且t≠1,n∈N*)
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式(用t,n表示)
(2)当t=2时,令cn= ![]() ,证明
,证明 ![]() ≤c1+c2+c3+…+cn<1.
≤c1+c2+c3+…+cn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinxcosx﹣ ![]() acos2x+
acos2x+ ![]() a+b(a>0)
a+b(a>0)
(1)写出函数的单调递减区间;
(2)设x∈[0, ![]() ],f(x)的最小值是﹣2,最大值是
],f(x)的最小值是﹣2,最大值是 ![]() ,求实数a,b的值.
,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的水平都比较稳定,若三人各自独立地进行一次投篮测试,则甲投中而乙不投中的概率为 ![]() ,乙投中而丙不投中的概率为
,乙投中而丙不投中的概率为 ![]() ,甲、丙两人都投中的概率为
,甲、丙两人都投中的概率为 ![]() .
.
(1)分别求甲、乙、丙三人各自投篮一次投中的概率;
(2)若丙连续投篮5次,求恰有2次投中的概率;
(3)若丙连续投篮3次,每次投篮,投中得2分,未投中得0分,在3次投篮中,若有2次连续投中,而另外1次未投中,则额外加1分;若3次全投中,则额外加3分,记ξ为丙连续投篮3次后的总得分,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足bcosA=(2c+a)cos(π﹣B)
(1)求角B的大小;
(2)若b=4,△ABC的面积为 ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足 ![]() =
= ![]() (0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( ) 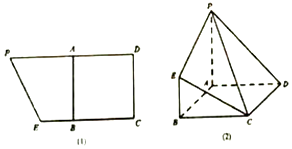
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA﹣csinC=(a﹣b)sinB.
(1)求角C的大小;
(2)若边长 ![]() ,求△ABC的周长最大值.
,求△ABC的周长最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com