
【题目】已知数列{an}的前n项和为Sn , 满足Sn= ![]() an﹣n(t>0且t≠1,n∈N*)
an﹣n(t>0且t≠1,n∈N*)
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式(用t,n表示)
(2)当t=2时,令cn= ![]() ,证明
,证明 ![]() ≤c1+c2+c3+…+cn<1.
≤c1+c2+c3+…+cn<1.
【答案】
(1)证明:∵数列{an}的前n项和为Sn,满足Sn= ![]() an﹣n(t>0且t≠1,n∈N*),
an﹣n(t>0且t≠1,n∈N*),
∴由题意当n=1时,a1=t﹣1,
∵Sn= ![]() an﹣n,①
an﹣n,①
∴Sn+1= ![]() an+1﹣(n+1),②
an+1﹣(n+1),②
②﹣①得an+1=tan+t﹣1,即an+1+1=t(an+1),
∴{an+1}是以t为首项,以t为公比的等比数列
∴数列{an}的通项公式 ![]()
(2)证明: ![]() =
= ![]() =
= ![]()
令Tn=c1+c2+c3+…+cn,
则Tn=(1﹣ ![]() )+(
)+( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )=1﹣
)=1﹣ ![]() .
.
∵Tn单调递增,∴当n=1时,(Tn)min= ![]() ,当n趋向无穷大时,Tn趋近1.
,当n趋向无穷大时,Tn趋近1.
∴ ![]() ≤c1+c2+c3+…+cn<1
≤c1+c2+c3+…+cn<1
【解析】(1)当n=1时,a1=t﹣1,an+1+1=t(an+1),由此能证明{an+1}是以t为首项,以t为公比的等比数列,并能求出数列{an}的通项公式.(2) ![]() =
= ![]() ,利用裂项求和法求出Tn=c1+c2+c3+…+cn=1﹣
,利用裂项求和法求出Tn=c1+c2+c3+…+cn=1﹣ ![]() ,由此能证明
,由此能证明 ![]() ≤c1+c2+c3+…+cn<1.
≤c1+c2+c3+…+cn<1.
【考点精析】通过灵活运用等比数列的通项公式(及其变式),掌握通项公式:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若△ABC的内角A,B,C的对边分别为a,b,c,已知c=2,C= ![]() .
.
(1)若b= ![]() ,求角B;
,求角B;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段A B两端点A和B分别在x轴和y轴上滑动,线段AB的中点M的轨迹为曲线C. (Ⅰ)求曲线C的方程;
(Ⅱ)点P(x,y)是曲线C上的动点,求3x﹣4y的取值范围;
(Ⅲ)已知定点Q(0, ![]() ),探究是否存在定点T(0,t)(t
),探究是否存在定点T(0,t)(t ![]() )和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
)和常数λ满足:对曲线C上任意一点S,都有|ST|=λ|SQ|成立?若存在,求出t和λ;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求y关于x的线性回归方程 ![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式: ![]() =
= 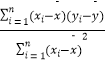 =
= 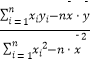 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{ an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{ an}的通项公式;
(2)若数列{bn}满足 ![]() +…+
+…+ ![]() =an (n∈N* ) 求数列{bn}的前n项和Sn .
=an (n∈N* ) 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列不等式中正确的是( )
A.sin ![]() π>sin
π>sin ![]() π
π
B.tan ![]() π>tan(﹣
π>tan(﹣ ![]() )
)
C.sin(﹣ ![]() )>sin(﹣
)>sin(﹣ ![]() )
)
D.cos(﹣ ![]() π)>cos(﹣
π)>cos(﹣ ![]() π)
π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com