
分析 根据题意,令An=$\frac{{n}^{2}}{100}$,显然0≤An≤100,依次讨论An的值,结合An=$\frac{{n}^{2}}{100}$求出n的值,最后讨论An的不同数值,即可得答案.
解答 解:根据题意,令An=$\frac{{n}^{2}}{100}$,显然0≤An≤100,
若An=0,即0≤$\frac{{n}^{2}}{100}$<1,解可得:n=1、2、3、…9,
若An=1,即1≤$\frac{{n}^{2}}{100}$<2,解可得:n=10、11、…14,
若An=2,即2≤$\frac{{n}^{2}}{100}$<3,解可得:n=15、16、17,
若An=3,即3≤$\frac{{n}^{2}}{100}$<4,解可得:n=18、19,
若An=4,即4≤$\frac{{n}^{2}}{100}$<5,解可得:n=20、21、22,
若An=5,即5≤$\frac{{n}^{2}}{100}$<6,解可得:n=23、24,
若An=6,即6≤$\frac{{n}^{2}}{100}$<7,解可得:n=25、26,
若An=7,即7≤$\frac{{n}^{2}}{100}$<8,解可得:n=27、28,
若An=8,即8≤$\frac{{n}^{2}}{100}$<9,解可得:n=29,
若An=9,即9≤$\frac{{n}^{2}}{100}$<10,解可得:n=30、31,
若An=10,即10≤$\frac{{n}^{2}}{100}$<11,解可得:n=32、33,
若An=11,即11≤$\frac{{n}^{2}}{100}$<12,解可得:n=34,
若An=12,即12≤$\frac{{n}^{2}}{100}$<13,解可得:n=35、36,
若An=13,即13≤$\frac{{n}^{2}}{100}$<14,解可得:n=37,
若An=14,即14≤$\frac{{n}^{2}}{100}$<15,解可得:n=38,
若An=15,即15≤$\frac{{n}^{2}}{100}$<16,解可得:n=39,
若An=16,即16≤$\frac{{n}^{2}}{100}$<17,解可得:n=40、41,
若An=17,即17≤$\frac{{n}^{2}}{100}$<18,解可得:n=42,
若An=18,即18≤$\frac{{n}^{2}}{100}$<19,解可得:n=43,
若An=19,即19≤$\frac{{n}^{2}}{100}$<20,解可得:n=44,
若An=20,即20≤$\frac{{n}^{2}}{100}$<21,解可得:n=45,
若An=21,即21≤$\frac{{n}^{2}}{100}$<22,解可得:n=46
若An=22,即22≤$\frac{{n}^{2}}{100}$<23,解可得:n=47,
若An=23,即23≤$\frac{{n}^{2}}{100}$<24,解可得:n=48,
若An=24,即24≤$\frac{{n}^{2}}{100}$<25,解可得:n=49,
当n≥50时,(n+1)2-n2=2n+1>100,即当n≥50时,每一个n对应一个[$\frac{{n}^{2}}{100}$]的值,
故一共有25+51=76个不同的数值,即组成集合A的元素的个数是76;
故答案为:76.
点评 本题考查元素与集合的关系,关键是理解[x]的定义,进而分类讨论,分析组成集合A的元素的情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
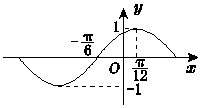 已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=sin({x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{2π}{3}})$ | D. | $y=sin({2x+\frac{π}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{E}{2},\frac{D}{2}})$ | B. | $({-\frac{E}{2},-\frac{D}{2}})$ | C. | $({\frac{D}{2},\frac{E}{2}})$ | D. | $({-\frac{D}{2},-\frac{E}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com