
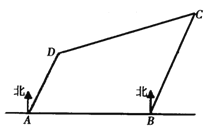
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
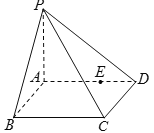
【题目】如图,四棱锥![]() 中,
中,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,四棱锥外接球的球心为
,四棱锥外接球的球心为![]() ,点
,点![]() 是棱
是棱![]() 上的一个动点.给出如下命题:①直线
上的一个动点.给出如下命题:①直线![]() 与直线
与直线![]() 所成的角中最小的角为
所成的角中最小的角为![]() ;②
;②![]() 与
与![]() 一定不垂直;③三棱锥
一定不垂直;③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确命题的序号是__________.(将你认为正确的命题序号都填上)
.其中正确命题的序号是__________.(将你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(Ⅱ)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年五月最受七中学子期待的学生活动莫过于学生节,在每届学生节活动中,着七中校服的布偶“七中熊”尤其受同学和老师欢迎.已知学生会将在学生节当天售卖“七中熊”,并且会将所获得利润全部捐献于公益组织.为了让更多同学知晓,学生会宣传部需要前期在学校张贴海报宣传,成本为250元,并且当学生会向厂家订制![]() 只“七中熊”时,需另投入成本
只“七中熊”时,需另投入成本![]() ,
,![]() (元),
(元),![]() .通过市场分析, 学生会订制的“七中熊”能全部售完.若学生节当天,每只“七中熊”售价为70元,则当销量为______只时,学生会向公益组织所捐献的金额会最大.
.通过市场分析, 学生会订制的“七中熊”能全部售完.若学生节当天,每只“七中熊”售价为70元,则当销量为______只时,学生会向公益组织所捐献的金额会最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() ,
,![]() .
.
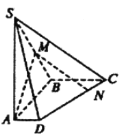
(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在第(2)问条件下,设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求当
,求当![]() 取最大值时点
取最大值时点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列:![]() ,满足:
,满足:![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为2的等比数列.
是公比为2的等比数列.
(1)若![]() ,求数列
,求数列![]() 的所有项的和
的所有项的和![]() ;
;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在正整数![]() ,满足
,满足![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 分别为棱
分别为棱![]() 上的动点(
上的动点(![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.
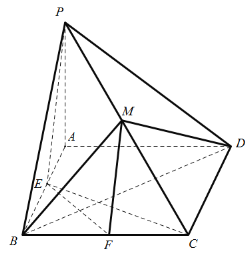
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某银行推出一款短期理财产品,约定如下:
(1)购买金额固定;
(2)购买天数可自由选择,但最短3天,最长不超过10天;
(3)购买天数![]() 与利息
与利息![]() 的关系,可选择下述三种方案中的一种:
的关系,可选择下述三种方案中的一种:
方案一:![]() ;方案二:
;方案二:![]() ;方案三:
;方案三:![]() .
.
请你根据以上材料,研究下面两个问题:
(1)结合所学的数学知识和方法,用其它方式刻画上述三种方案的函数特征;
(2)依据你的分析,给出一个最佳理财方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com