
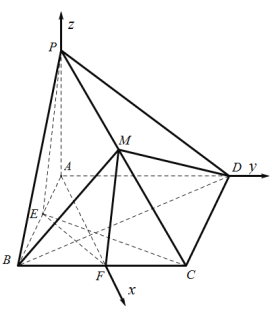
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 分别为棱
分别为棱![]() 上的动点(
上的动点(![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.
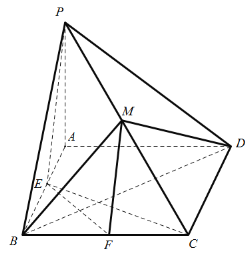
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接AC交BD于N,连接MN,证明MN∥PA,AC⊥MN得到AC⊥平面MBD,再根据EF∥AC得到证明.
(2)设BE=BF=x,由![]() ,得到E,F分别为棱AB,BC的中点时体积最大,以A为坐标原点,分别以AF,AD,AP所在直线为x,y,z轴建立空间直角坐标系,计算平面MEF和平面MEC的法向量,计算向量夹角得到答案.
,得到E,F分别为棱AB,BC的中点时体积最大,以A为坐标原点,分别以AF,AD,AP所在直线为x,y,z轴建立空间直角坐标系,计算平面MEF和平面MEC的法向量,计算向量夹角得到答案.
(1)连接AC交BD于N,连接MN,
∵底面ABCD为正方形,∴AC⊥BD,AN=NC,又∵PM=MC,∴MN∥PA,
由PA⊥底面ABCD知,MN⊥底面ABCD,又AC底面ABCD,∴AC⊥MN,
又BD∩MN=N,BD,MN平面MBD,∴AC⊥平面MBD,
在△ABC中,∵BE=BF,BA=BC,∴![]() ,即EF∥AC,
,即EF∥AC,
∴EF⊥平面MBD,又EF平面PEF,∴平面PEF⊥平面MBD;
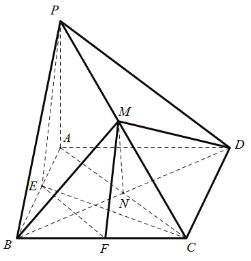
(2)设BE=BF=x,由题意![]() ,又PA=4,
,又PA=4,
∴![]() ,当x=2时,三棱锥F﹣PEC的体积最大.
,当x=2时,三棱锥F﹣PEC的体积最大.
即此时E,F分别为棱AB,BC的中点.
以A为坐标原点,分别以AF,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
则C(![]() ,2,0),F(2
,2,0),F(2![]() ,0,0),E(
,0,0),E(![]() ,
,![]() ,0),M(
,0),M(![]() ,1,2),
,1,2),
![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
取![]() =1,得:
=1,得:![]() ,
,
设![]() 为平面MEC的一个法向量,则
为平面MEC的一个法向量,则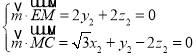 ,
,
取![]() =1,得:
=1,得:![]() ,则
,则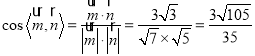 ,
,
由图知所求二面角为锐二面角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
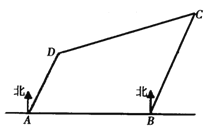
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面几种说法:
①相等向量的坐标相同;
②若向量![]() 满足
满足![]() ,则
,则![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共线的四点,则“
是不共线的四点,则“![]() ”是“四边形
”是“四边形![]() 为平行四边形”的充要条件;
为平行四边形”的充要条件;
④![]() 的充要条件是
的充要条件是![]() 且
且![]() .
.
其中正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
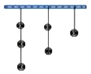
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com