
【题目】设数列{an}的前n项和Sn满足:Sn=nan﹣2n(n﹣1),首项![]() =1.
=1.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Mn,求证:
的前n项和为Mn,求证:![]()
![]() Mn
Mn![]()
![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中m,n,k∈R.
,其中m,n,k∈R.
(1)若m=n=k=1,求f(x)的单调区间;
(2)若n=k=1,且当x≥0时,f(x)≥1总成立,求实数m的取值范围;
(3)若m>0,n=0,k=1,若f(x)存在两个极值点x1、x2 , 求证: ![]() <f(x1)+f(x2)<
<f(x1)+f(x2)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a+b)cosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)求sinAcosB的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex﹣x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED= ![]() ,EC=
,EC= ![]() .
. 
(Ⅰ)求sin∠BCE的值;
(Ⅱ)求CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆x2+y2﹣2x+10y﹣24=0和 x2+y2+2x+2y﹣8=0
(1)判断两圆的位置关系;(2)求公共弦所在的直线方程及公共弦的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求BD1与平面A1BC1所成角的正弦值.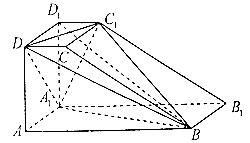
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com