
【题目】已知函数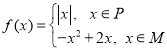 ,其中
,其中![]() 、
、![]() 是非空数集,且
是非空数集,且![]() ,设
,设![]() ,
,![]() ;
;
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)是否存在实数![]() ,使得
,使得![]() ,且
,且![]() ?若存在,请求出满足条件的实数
?若存在,请求出满足条件的实数![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若![]() ,且
,且![]() ,
,![]() ,
,![]() 是单调递增函数,求集合
是单调递增函数,求集合![]() 、
、![]() ;
;
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ,其中
,其中![]() 或者
或者![]() ,其中
,其中![]() 或者
或者
![]() 或者
或者![]()
【解析】
(1)根据![]() ,
,![]() 分别代入对应的分段区间求解集合的范围再求并集即可.
分别代入对应的分段区间求解集合的范围再求并集即可.
(2)先假设![]() 推出矛盾,故可得
推出矛盾,故可得![]() .代入可得
.代入可得![]() ,再分析当
,再分析当![]() 时与题设矛盾可得
时与题设矛盾可得![]() .
.
(3)先根据函数的单调性确定![]() ,
,![]() ,再证明在
,再证明在![]() 上存在分界点的话,这个分界点应该满足的性质,最后根据此性质写出满足题意的集合即可.
上存在分界点的话,这个分界点应该满足的性质,最后根据此性质写出满足题意的集合即可.
(1)因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
故![]() .
.
(2)若![]() ,则
,则![]() ,不符合要求.
,不符合要求.
所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,解得
,解得![]() .
.
若![]() 则
则 ![]() .
.
因为![]() ,所以
,所以![]() 的原象
的原象![]() 且
且![]()
所以![]() ,得
,得![]() ,与前提矛盾.
,与前提矛盾.
故![]()
(3)因为![]() 是单调递增函数,所以对任意的
是单调递增函数,所以对任意的![]() 有
有![]() ,所以
,所以![]()
所以![]() ,同理可证
,同理可证![]() .若存在
.若存在![]() ,使得
,使得![]() ,
,
则![]() ,于是
,于是![]() ,
,
记![]() ,
,![]()
所以![]() ,同理可知
,同理可知![]() …
…
由![]() ,得
,得![]() ,
,
所以![]() .
.
所以![]() ,故
,故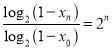 ,
,
即![]() ,此时
,此时![]() .
.
对于任意![]() ,取
,取![]() 中的自然数
中的自然数![]() ,
,
则![]() .所以
.所以![]() .
.
综上所述,满足要求的![]() 必有如下表示:
必有如下表示:
![]() ,其中
,其中![]() 或者
或者
![]() ,其中
,其中![]() 或者
或者
![]() 或者
或者![]()


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明用数列{an}记录某地区2019年12月份31天中每天是否下过雨,方法为:当第k天下过雨时,记ak=1,当第k天没下过雨时,记ak=﹣1(1≤k≤31);他用数列{bn}记录该地区该月每天气象台预报是否有雨,方法为:当预报第k天有雨时,记bk=1,当预报第k天没有雨时,记bk=﹣1(1≤k≤31);记录完毕后,小明计算出a1b1+a2b2+…+a31b31=25,那么该月气象台预报准确的的总天数为_____;若a1b1+a2b2+…+akbk=m,则气象台预报准确的天数为_____(用m,k表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念越来越深入人心,据此,某网站调查了人们对生态文明建设的关注情况,调查数据表明,参与调查的人员中关注生态文明建设的约占80%.现从参与调查的关注生态文明建设的人员中随机选出200人,并将这200人按年龄(单位:岁)分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65],得到的频率分布直方图如图所示.
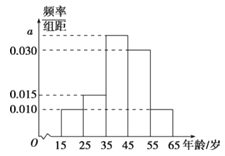
(Ⅰ)求这200人的平均年龄(每一组用该组区间的中点值作为代表)和年龄的中位数(保留一位小数);
(Ⅱ)现在要从年龄在第1,2组的人员中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求抽取的3人中恰有2人的年龄在第2组中的概率;
(Ⅲ)若从所有参与调查的人(人数很多)中任意选出3人,设这3人中关注生态文明建设的人数为X,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 有唯一实数解,试求实数
有唯一实数解,试求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且不等式
,且不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com